a) Vẽ đồ thị các hàm số y = x + 2 và y = -x + 4 trên cùng hệ tọa độ.
b) Gọi giao điểm của 2 đường thẳng trên là A và giao điểm của chúng với trục hoành lần lượt là B và C. Tìm tọa độ A, B, C.
c) Chứng tỏ tam giác ABC vuông cân.
a) Vẽ đồ thị các hàm số y=-x+4(d1) và y=x-4(d2) trên cùng một mặt phẳng tọa độ.
b) Gọi A, B lần lượt là giao điểm của các đường thẳng (d1);(d2) với trục tung và giao điểm của 2 đường thẳng là C. Tìm tọa độ giao điểm A,B,C.
c) Tính S tam giác ABC
b) Phương trình hoành độ giao điểm của (D1) và (d2) là:
-x+4=x-4
\(\Leftrightarrow-2x=-8\)
hay x=4
Thay x=4 vào (d1), ta được:
y=-4+4=0
Thay x=0 vào (d1), ta được:
\(y=-0+4=4\)
Thay x=0 vào (d2), ta được:
\(y=0-4=-4\)
Vậy: A(0;4); B(0;-4); C(4;0)
Cho hàm số y=3x-1 có đồ thị d1 và hàm số y=-x +3 có đồ thị d2 A. Vẽ đồ thị hs trên cùng hệ trục tọa độ Oxy B. Gọi giao điểm d1, d2 với trục Õ lần lượt là A và B, giao điểm của 2 đường thẳng d1 và d2 là C. Tìm tọa độ các điểm A,B,C C. Tính số đo của góc tạo bởi đường thẳng d1 với tia Ox
a: 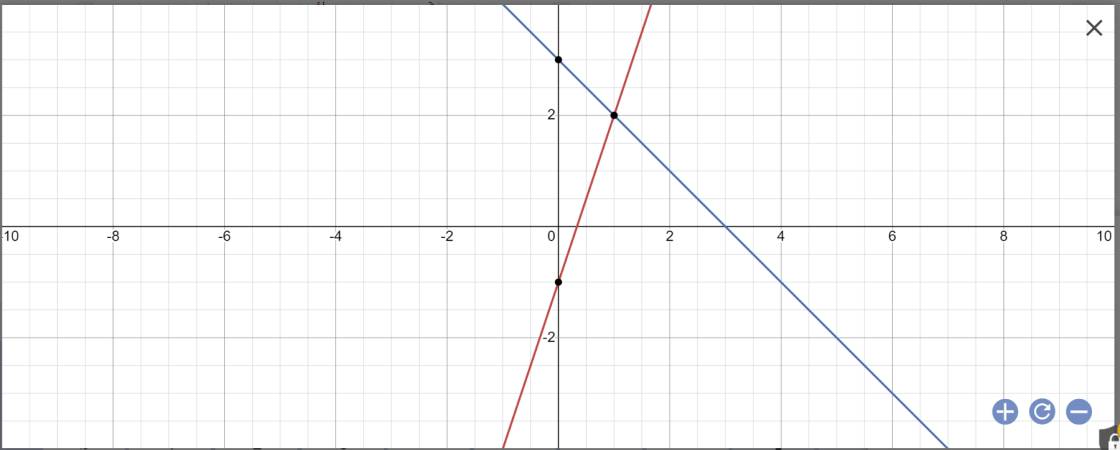
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\3x-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=0\end{matrix}\right.\)
Vậy: A(1/3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-x=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)
Vậy: B(3;0)
Tọa độ C là:
\(\left\{{}\begin{matrix}3x-1=-x+3\\y=3x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x=4\\y=3x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-1=2\end{matrix}\right.\)
Vậy: C(1;2)
c: Gọi \(\alpha\) là góc tạo bởi (d1) với trục Ox
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^033'\)
a, Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau : y=x+2 và y=-2x + 5
b, Gọi giao điểm của các đường thẳng y = x+2 và y = -2x+5 với trục hoành theo thứ tự là A và B , gọi giao điểm của 2 đường thẳng trên là C.Tìm tọa độ của điểm C.Tính Chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là cm và làm tròn đến chữ số thập phân thứ 2 )
Các bác jup e vs
b) Vì C(xC,yC) là giao điểm của hai đường thẳng y=x+2 và y=-2x+5 nên hoành độ của C là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của y=x+2 và y=-2x+5
hay x+2=-2x+5
\(\Leftrightarrow x+2+2x-5=0\)
\(\Leftrightarrow3x-3=0\)
\(\Leftrightarrow3x=3\)
hay x=1
Thay x=1 vào hàm số y=x+2, ta được:
y=1+2=3
Vậy: C(1;3)
Vì A(xA;yA) là giao điểm của đường thẳng y=x+2 với trục hoành nên yA=0
Thay y=0 vào hàm số y=x+2, ta được:
x+2=0
hay x=-2
Vậy: A(-2:0)
Vì B(xB,yB) là giao điểm của đường thẳng y=-2x+5 với trục hoành Ox nên yB=0
Thay y=0 vào hàm số y=-2x+5, ta được:
-2x+5=0
\(\Leftrightarrow-2x=-5\)
hay \(x=\dfrac{5}{2}\)
Vậy: \(B\left(\dfrac{5}{2};0\right)\)
Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(xA-xB\right)^2+\left(yA-yB\right)^2}\)
\(\Leftrightarrow AB=\sqrt{\left(-2-\dfrac{5}{2}\right)^2+\left(0-0\right)^2}\)
\(\Leftrightarrow AB=\sqrt{\left(-\dfrac{9}{2}\right)^2}=\dfrac{9}{2}=4,5\left(cm\right)\)
Độ dài đoạn thẳng AC là:
\(AC=\sqrt{\left(xA-xC\right)^2+\left(yA-yC\right)^2}\)
\(\Leftrightarrow AC=\sqrt{\left(-2-1\right)^2+\left(0-3\right)^2}\)
\(\Leftrightarrow AC=\sqrt{18}=3\sqrt{2}\left(cm\right)\)
Độ dài đoạn thẳng BC là:
\(BC=\sqrt{\left(xB-xC\right)^2+\left(yB-yC\right)^2}\)
\(\Leftrightarrow BC=\sqrt{\left(\dfrac{5}{2}-1\right)^2+\left(0-3\right)^2}\)
\(\Leftrightarrow BC=\sqrt{\dfrac{45}{4}}=\dfrac{3\sqrt{5}}{2}\left(cm\right)\)
Chu vi của tam giác ABC là:
\(C_{ABC}=AB+AC+BC\)
\(\Leftrightarrow C_{ABC}=4.5+3\sqrt{2}+\dfrac{3\sqrt{5}}{2}\simeq12.10cm\)
Nửa chu vi của tam giác ABC là:
\(P_{ABC}=\dfrac{C_{ABC}}{2}\simeq\dfrac{12.10}{2}=6.05cm\)
Diện tích của tam giác ABC là:
\(S_{ABC}=\sqrt{P\cdot\left(P-AB\right)\cdot\left(P-BC\right)\cdot\left(P-AC\right)}\)
\(=\sqrt{6.05\cdot\left(6.05-4.5\right)\cdot\left(6.05-3\sqrt{2}\right)\cdot\left(6.05-\dfrac{3\sqrt{5}}{2}\right)}\)
\(\simeq6.76cm^2\)
cho hàm số y=x 4 và y=-x 2
a,vẽ đồ thị của 2 hàm số trên cùng 1 hệ trục tọa độ
b,gọi A là giao điểm của hai đường thẳng trên,B và C lần lượt là giao điểm của 2 đường thẳng đó với trục Ox.Tính chu vi và diện tích của tam giác ABC
Bạn nhập lại hai hàm số đó nhé chính giữa mik không biết là dấu + hay -
Cho hàm số y = 2x và y = -3x + 5
a) Vẽ trên cùng một hệ trục tọa độ, đồ thị hai hàm số trên?
b) Tìm tọa độ giao điểm M của hai đồ thị bằng phương pháp đại số. Gọi A, B lần lượt là giao điểm của đường thẳng y = -3x + 5 với trục hoành và trục tung. Tính diện tích tam giác OAB và diện tích tam giác OMA.
Cho hàm số y = x + 2 và hàm số y = 3 − x có đồ thị là (d1) và )(d2).
a) Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (d1) với trục hoành.
c) Tìm tọa độ giao điểm của (d2) với trục tung.
d) Tìm tọa độ giao điểm của (d1) và (d2).
Cho hai hàm số : y = -2x + 4 (d1)
y = x + 1 (d2)
a. Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ
b. gọi A là tọa độ giao điểm của 2 đường thẳng.B , C là giao điểm của (d1) và (d2) với trục hoành. Tìm tọa độ A,B,C.
\(b,\) Tọa độ giao điểm 2 đường thẳng là:
\(\left\{{}\begin{matrix}y=-2x+4\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+1=-2x+4\\y=x+1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\Leftrightarrow A\left(1;2\right)\)
Tọa độ giao điểm 2 đường thẳng với trục hoành là
\(\left\{{}\begin{matrix}y=0\\\left[{}\begin{matrix}y=-2x+4\\y=x+1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\\left[{}\begin{matrix}4-2x=0\\x+1=0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow B\left(2;0\right),C\left(-1;0\right)\)
Bài 1: Vẽ các đồ thị hàm số sau trên cùng 1 hệ trục tọa độ \(y=-x+5\)(1); \(y=4x\)(2); \(y=\dfrac{-1}{4}x\)(3)
b, Gọi giao điểm của đường thẳng có phương trình (1) với các đường thẳng có phương trình (2) và (3) lần lượt tại A và B. Tìm tọa độ các điểm A và B
c, Tam giác OAB là tam giác gì? Vì sao?
d, Tính \(S_{AOB}\)
a:
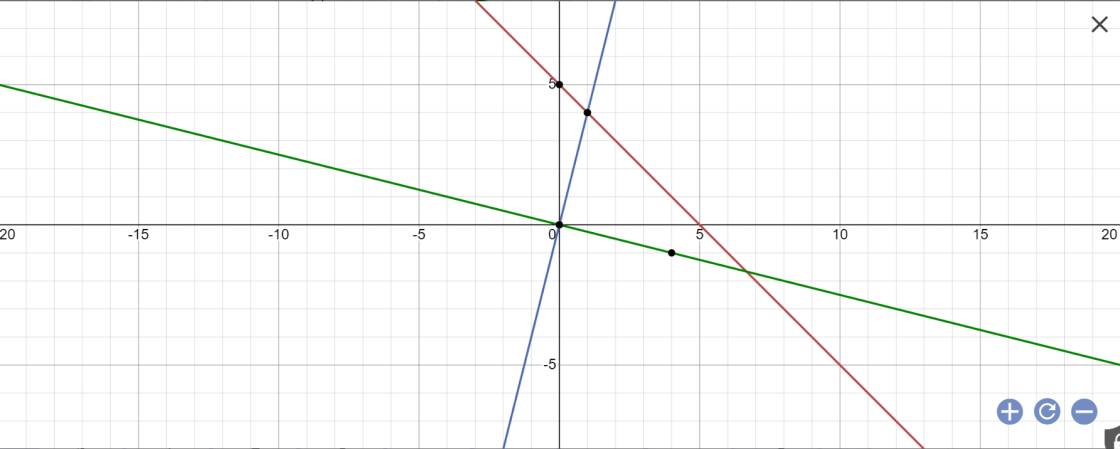
b: tọa độ A là;
-x+5=4x và y=4x
=>x=1 và y=4
Tọa độ B là;
-x+5=-1/4x và y=-1/4x
=>-3/4x=-5 và y=-1/4x
=>x=5:3/4=5*4/3=20/3 và y=-1/4*20/3=-5/3
=>B(20/3;-5/3)
c: O(0;0); A(1;4); B(20/3;-5/3)
\(OA=\sqrt{1^2+4^2}=\sqrt{17}\)
\(OB=\sqrt{\left(\dfrac{20}{3}\right)^2+\left(-\dfrac{5}{3}\right)^2}=\dfrac{5\sqrt{17}}{3}\)
\(AB=\sqrt{\left(\dfrac{20}{3}-1\right)^2+\left(-\dfrac{5}{3}-4\right)^2}=\dfrac{\sqrt{818}}{3}\)
\(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=\dfrac{-8}{17}\)
=>góc AOB tù
=>ΔOAB tù
Cho 2 hàm số y=2,5x+3 và y=-0,5x+1,5
a) Vẽ đồ thị của 2 hàm số trên cùng 1 trục tọa độ
b) Gọi giao điểm của các đường thẳng y=2,5x+3 và y=-0,5x+1,5 với trục hoành theo thứ tự và gọi giao điểm của 2 đường thẳng đó là C. Tìm tọa độ của điểm A, B, C
c) Tính góc tạo bởi các đường thẳng y=2,5x+3 và y=-0,5x+1,5 và trục Ox (làm tròn đến độ)
d) Tính chu vi và diện tích △ABC
e) Tính các góc của △ABC
b: Tọa độ điểm C là:
\(\left\{{}\begin{matrix}2.5x+3=-0.5x+1.5\\y=2.5x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=-1.5\\y=2.5x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{5}{2}\cdot\dfrac{-1}{2}+3=3-\dfrac{5}{4}=\dfrac{7}{4}\end{matrix}\right.\)