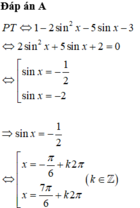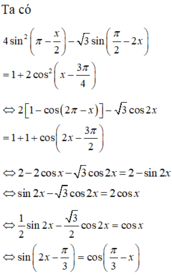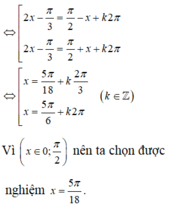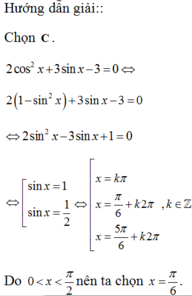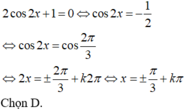Nghiệm của phương trình cos^2x+2cos2x-3=0 là

Những câu hỏi liên quan
Tính tổng S các nghiệm của phương trình \(\left(2cos2x+5\right)\left(sin^4x-cos^4x\right)+3=0\) trong khoảng \(\left(0;2\pi\right)\)
Cho hai phương trình cos 3x -1 0 (1); cos 2x
-
1
2
(2) Tập các nghiệm của phương trình (1) đồng thời là nghiệm của phương trình (2) là
Đọc tiếp
Cho hai phương trình cos 3x -1 =0 (1); cos 2x = - 1 2 (2) Tập các nghiệm của phương trình (1) đồng thời là nghiệm của phương trình (2) là
![]()
![]()
![]()
![]()
Đáp án D
Ta có
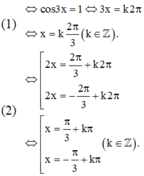
Suy ra nghiệm chung của hai phương trình là
![]()
Đúng 0
Bình luận (0)
Nghiệm của phương trình cos 2x – 5. sin x – 3 0 là:
Đọc tiếp
Nghiệm của phương trình cos 2x – 5. sin x – 3 = 0 là:
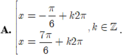
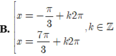
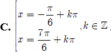
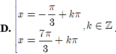
Nghiệm của phương trình
cos
2
x
+
3
sin
x
-
2
cos
x
0
là
Đọc tiếp
Nghiệm của phương trình cos 2 x + 3 sin x - 2 cos x = 0 là
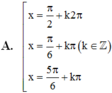
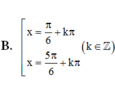
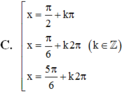
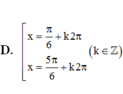
Đáp án D
Tìm điều kiện để phương trình có nghĩa. Sau đó sử dụng công thức 2 cos 2 x = 1 - 2 sin 2 x để đưa phương trình đã cho về phương trình bậc 2 đối với sin x và giải phương trình này để tìm nghiệm. Bước cuối cùng là đối chiếu điều kiện để kết luận nghiệm.
Điều kiện
![]()
Với điều kiện trên phương trình đã cho trở thành
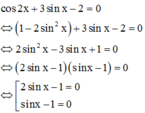
Nếu
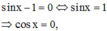
không thỏa mãn điều kiện (1)
Vậy
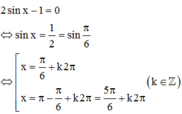
Đúng 0
Bình luận (0)
Tìm nghiệm x
∈
0
;
π
2
của phương trình sau
4
sin
2
π
-
π
2
-
3
sin
π
2
-
2...
Đọc tiếp
Tìm nghiệm x ∈ 0 ; π 2 của phương trình sau 4 sin 2 π - π 2 - 3 sin π 2 - 2 x = 1 + 2 cos 2 x - π 4
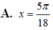
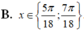
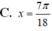
![]()
Tìm các nghiệm
x
∈
0
;
π
2
của phương trình sau
4
sin
2
π
-
x
2
-
3
π
2
-
2
x...
Đọc tiếp
Tìm các nghiệm x ∈ 0 ; π 2 của phương trình sau
4 sin 2 π - x 2 - 3 π 2 - 2 x = 1 + 2 cos 2 x - 3 π 4
A. x = 5 π 8
B. x ∈ 5 π 18 ; 7 π 18
C. x = 7 π 18
D. x ∈ ∅
Ta có:
4 sin 2 π - x 2 - 3 π 2 - 2 x = 1 + 2 cos 2 x - 3 π 4 ⇔ 2 1 - cos 2 π - x - 3 cos 2 x = 1 + 1 + cos 2 x - 3 π 2 ⇔ 2 - 2 cos x - 3 cos 2 x = 2 - sin 2 x ⇔ sin 2 x - 3 cos 2 x = 2 cos x ⇔ 1 2 sin 2 x - 3 2 cos 2 x = cos x ⇔ sin 2 x - π 3 = cos π 3 - x ⇔ x = 5 π 8 + k 2 π 3 x = 5 π 6 + k 2 π
Vì x ∈ 0 ; π 2 nên ta chọn được nghiệm x = 5 π 8
Đáp án A
Đúng 0
Bình luận (0)
Nghiệm của phương trình lượng giác: 2cos2x + 3sinx – 3 0 thõa mãn điều kiện
0
x
π
2
là: A. x
π
/3 B. x
π
/2 C. x
π
/6 D. x 5
π
/6
Đọc tiếp
Nghiệm của phương trình lượng giác: 2cos2x + 3sinx – 3= 0 thõa mãn điều kiện 0 < x < π 2 là:
A. x = π /3
B. x = π /2
C. x = π /6
D. x = 5 π /6
Nghiệm của phương trình 2cos2x + 1 = 0 là:
![]()
![]()
![]()
Tổng S các nghiệm của phương trình
2
.
cos
2
2
x
+
5
.
cos
2
x
-
3
0
trong khoảng
0
,
2
π
là
Đọc tiếp
Tổng S các nghiệm của phương trình 2 . cos 2 2 x + 5 . cos 2 x - 3 = 0 trong khoảng 0 , 2 π là
![]()
![]()
![]()
![]()