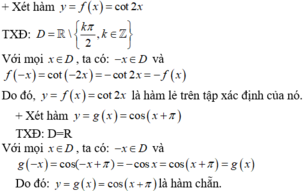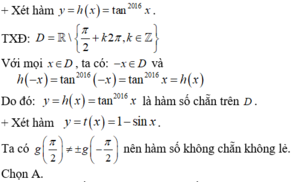Tập xác định của hàm số là y = cos(2x - pi/3)

Những câu hỏi liên quan
Khẳng định nào sau đây là sai?
A. Hàm số \(y = \cos x\) có tập xác định là \(\mathbb{R}\)
B. Hàm số \(y = \cos x\) có tập giá trị là [-1;1]
C. Hàm số \(y = \cos x\) là hàm số lẻ
D. Hàm số \(y = \cos x\) tuần hoàn với chu kỳ \(2\pi \)
Ta có: \(y = \cos x\)
\(y\left( { - x} \right) = \cos \left( { - x} \right) = \cos x = y\)
Suy ra hàm số \(y = \cos x\) là hàm số chẵn
Vậy ta chọn đáp án C
Đúng 0
Bình luận (0)
tìm tập xác định của hàm số lượng giác saua)ydfrac{tanleft(2x-dfrac{pi}{4}right)}{sqrt{1-sinleft(x-dfrac{pi}{8}right)}}b)ydfrac{tanleft(x-dfrac{pi}{4}right)}{1-cosleft(x+dfrac{pi}{3}right)}c)ydfrac{3}{cosx-cos3x}d)ydfrac{4}{sin^2x-cos^2x}e)ydfrac{1+cotleft(dfrac{pi}{3}+xright)}{tan^2left(3x-dfrac{pi}{4}right)}
Đọc tiếp
tìm tập xác định của hàm số lượng giác sau
a)\(y=\dfrac{tan\left(2x-\dfrac{\pi}{4}\right)}{\sqrt{1-sin\left(x-\dfrac{\pi}{8}\right)}}\)
b)\(y=\dfrac{tan\left(x-\dfrac{\pi}{4}\right)}{1-cos\left(x+\dfrac{\pi}{3}\right)}\)
c)\(y=\dfrac{3}{cosx-cos3x}\)
d)\(y=\dfrac{4}{sin^2x-cos^2x}\)
e)\(y=\dfrac{1+cot\left(\dfrac{\pi}{3}+x\right)}{tan^2\left(3x-\dfrac{\pi}{4}\right)}\)
Tìm tập xác định của hàm số y = \(2tan^4\left(2x-\dfrac{\pi}{3}\right)\)
\(ĐKXĐ:2x-\dfrac{\pi}{3}\ne\dfrac{\pi}{2}+k\pi\left(k\in Z\right)\)
\(\Leftrightarrow2x\ne\dfrac{5\pi}{6}+k\pi\left(k\in Z\right)\)
\(\Leftrightarrow x\ne\dfrac{5\pi}{12}+\dfrac{k\pi}{2}\left(k\in Z\right)\)
TXĐ:\(D=R\ \)\\(\left\{\dfrac{5\pi}{12}+\dfrac{k\pi}{2}\text{|}k\in Z\right\}\)
Đúng 2
Bình luận (0)
tìm tập xác định của mỗi hàm số sau : a) y = \(\sqrt{\frac{1-\sin x}{1+\cos x}}\) ; b) y = \(\tan\left(2x+\frac{\pi}{3}\right)\).
a)\(\forall x\Rightarrow sinx\le1\Rightarrow1-sinx\ge0\)
cosx\(\ge-1\Rightarrow1+cosx\ge0\)
ĐK:cosx\(\ne-1\Leftrightarrow x\ne\pi+k2\pi\)
\(\Rightarrow D=\left\{R\backslash\left\{\pi+k2\pi\right\}\right\}\)
b)ĐK:\(cos\left(2x+\frac{\pi}{3}\right)\ne0\Leftrightarrow2x+\frac{\pi}{3}\ne\frac{\pi}{2}+k\pi\Leftrightarrow x\ne\frac{\pi}{12}+\frac{k\pi}{2}\)
\(\Rightarrow D=\left\{R\text{\}\left\{\frac{\pi}{12}+\frac{k\pi}{2}\right\}\right\}\)
Đúng 0
Bình luận (0)
Tìm tập xác định của hàm số
\(y=f\left(x\right)=\dfrac{\sqrt{4\pi^2-x^2}}{cos\left(x\right)}\)
Hàm số xác định khi: \(\left\{{}\begin{matrix}4\pi^2-x^2\ge0\\cosx\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2\pi\le x\le2\pi\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
Đúng 1
Bình luận (2)
Trong các hàm số sau, có bao nhiêu hàm số là hàm chẵn trên tập xác định của nó:
y
c
o
t
2
x
,
y
cos
(
x
+
π
)
,
y
1
-
sinx
,
y
tan
2016
x
A. 2 B. 1 C. 4 D. 3
Đọc tiếp
Trong các hàm số sau, có bao nhiêu hàm số là hàm chẵn trên tập xác định của nó: y = c o t 2 x , y = cos ( x + π ) , y = 1 - sinx , y = tan 2016 x
A. 2
B. 1
C. 4
D. 3
Trong các hàm số sau, có bao nhiêu hàm số là hàm chẵn trên tập xác định của nó?
y = cot 2x; y = cos ( x + π ) ; y=10 - sinx; y= 100 tan100x.
A. 1
B. 2
C.3
D. 4
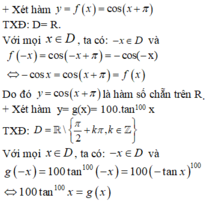
Do đó: y= 100 tan100x là hàm chẵn trên tập xác định của nó.
Đáp án B
Đúng 0
Bình luận (0)
Trong các hàm số sau, có bao nhiêu hàm số là hàm chẵn trên tập xác định của nó? y cot 2x; y cos(x + π); y 1 – sin x; y tan2016x A. 1. B. 2 C. 3 D. 4
Đọc tiếp
Trong các hàm số sau, có bao nhiêu hàm số là hàm chẵn trên tập xác định của nó?
y = cot 2x; y = cos(x + π); y = 1 – sin x; y = tan2016x
A. 1.
B. 2
C. 3
D. 4
Đáp án B
+ Xét hàm y = f(x) = cos (x + π)
TXĐ: D = R
Với mọi x ∈ D, ta có: -x ∈ D và f(-x) = cos (-x + π) = -cos x = cos (x + π) = f(x)
Do đó y = cos (x + π) là hàm số chẵn .
+ Xét hàm y = g(x) = tan2016x
TXĐ: D = R\{π/2 + kπ, k ∈ Z}
Với mọi x ∈ D, ta có: -x ∈ D và g(-x) = tan2016(-x) = (-tan x)2016 = tan2016x = g(x)
Do đó: y = tan2016x là hàm chẵn trên tập xác định của nó.
+Xét hàm y = cot2x
f(-x) = cot(-2x) = - cot 2x = -f(x) nên đây là hàm số lẻ.
+ Xét hàm số y = 1-sinx
f(-x) = 1- sin(-x) = 1+ sin x
Nên hàm số không chẵn không lẻ
Đúng 1
Bình luận (0)
Giải pt:1. (sqrt{9-x^2}-2x).(x^3+x^2-12x+10)0 2. cos3x+2cos^2(x+dfrac{pi}{6})1Bài 2 Tìm tập xác định của hàm số y dfrac{sqrt{1-sin2x}}{cos3x}Bài 3 : cho pt (cosx+1)(cos-2x-mcosx)msin^2 xtìm m để pt có đúng 2 nghiệm phân biệt thuộc [0;dfrac{2pi}{3}]bài 4: cho hàm số y x^3-2mx^2+(7m-8)x-5m10 có đồ thị (C_m) và đường thẳng d: yx+m. tìm m để d cắt ( C_m) tai ba điểm phân biêt giúp e với mn ơiiii
Đọc tiếp
Giải pt:
1. (\(\sqrt{9-x^2}\)-2x).(x\(^3\)+x\(^2\)-12x+10)=0 2. cos3x+2cos\(^2\)(x+\(\dfrac{\pi}{6}\))=1
Bài 2 Tìm tập xác định của hàm số y = \(\dfrac{\sqrt{1-sin2x}}{cos3x}\)
Bài 3 : cho pt (cosx+1)(cos-2x-mcosx)=msin\(^2\) x
tìm m để pt có đúng 2 nghiệm phân biệt thuộc \([0;\dfrac{2\pi}{3}\)\(]\)
bài 4: cho hàm số y= x\(^3\)-2mx\(^2\)+(7m-8)x-5m=10 có đồ thị (C\(_m\)) và đường thẳng d: y=x+m. tìm m để d cắt ( C\(_m\)) tai ba điểm phân biêt
giúp e với mn ơiiii