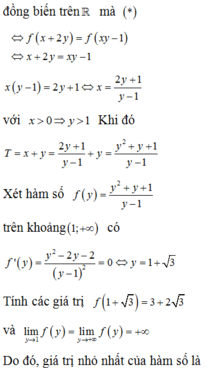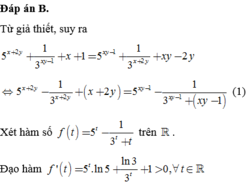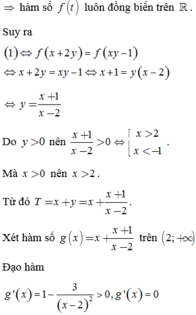Cho x,y là số thực thỏa mãn điều kiện x+y=1.Tìm giá trị nhỏ nhất của A= x^3+y^3

Những câu hỏi liên quan
cho hai số thực x,y thỏa mãn điều kiện x-3\(\sqrt{x+1}=3\sqrt{y+2}-y\).hãy tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức K=x+y
Cho x, y là các số thực thỏa mãn điều kiện x2 + y2= 1 .Tìm giá trị nhỏ nhất của biểu thức P = (3-x) χ (3-y)
( có thể dùng BĐT Bunhia copxki)
Do \(x^2+y^2=1\), đặt \(\left\{{}\begin{matrix}x=sina\\y=cosa\end{matrix}\right.\)
\(P=\left(3-sina\right)\left(3-cosa\right)=9-3\left(sina+cosa\right)+sina.cosa\)
Đặt \(sina+cosa=t\Rightarrow t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(t^2=1+2sina.cosa\Rightarrow sina.cosa=\dfrac{t^2-1}{2}\)
\(P=9-3t+\dfrac{t^2-1}{2}=\dfrac{1}{2}t^2-3t+\dfrac{17}{2}\)
Xét hàm \(f\left(t\right)=\dfrac{1}{2}t^2-3t+\dfrac{17}{2}\) trên \(\left[-\sqrt{2};\sqrt{2}\right]\)
\(f'\left(t\right)=t-3=0\Rightarrow t=3\notin\left[-\sqrt{2};\sqrt{2}\right]\)
\(f\left(-\sqrt{2}\right)=\dfrac{19+6\sqrt{2}}{2}\) ; \(f\left(\sqrt{2}\right)=\dfrac{19-6\sqrt{2}}{2}\)
\(\Rightarrow P_{min}=f\left(\sqrt{2}\right)=\dfrac{19-6\sqrt{2}}{2}\) khi \(t=\sqrt{2}\)
Đúng 1
Bình luận (0)
cho các số thực x và y thỏa mãn điều kiện \(x^2+y^2=2\)
tìm giá trị nhỏ nhất của biểu thức P=3(x+y)+xy
cho các số thực x và y thỏa mãn điều kiện x^2 + y^2 = 2 Tìm giá trị nhỏ nhất của biểu thức P = 3(x+y)+xy
cho x y z là ba số thực thay đổi thỏa mãn điều kiện x+y+z=3
tìm giá trị nhỏ nhất của biểu thức P= 1/căn x+ 1/căn y+ 1/căn z
Áp dụng BĐT Cô-si, ta có :
\(P=\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{z}}\ge3\sqrt[3]{\frac{1}{\sqrt{xyz}}}\)
Mặt khác, ta có : \(\sqrt[3]{xyz}\le\frac{x+y+z}{3}=1\)
\(\Rightarrow P\ge3\)
Vậy GTNN của P là 3 khi x = y = z = 1
Cách đơn giản hơn cách của anh Tùng:) sửa nốt là thực dương :V
Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(P=\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{z}}\ge\frac{\left(1+1+1\right)^2}{\sqrt{x}+\sqrt{y}+\sqrt{z}}=\frac{9}{\sqrt{x}+\sqrt{y}+\sqrt{z}}\)
Xét bđt phụ \(x+y+z\ge\sqrt{x}+\sqrt{y}+\sqrt{z}\)với x,y,z > 0 ( cấy ni thì dễ rồi nhân 2 vào cả 2 vế chuyển vế là xong )
\(\Rightarrow P\ge\frac{9}{\sqrt{x}+\sqrt{y}+\sqrt{z}}\ge\frac{9}{x+y+z}=\frac{9}{3}=3\)
Dấu "=" xảy ra <=> x=y=z=1
Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel kết hợp bất đẳng thức phụ \(x+y+z\ge\sqrt{x}+\sqrt{y}+\sqrt{z}\)ta có :
\(P\ge\frac{\left(1+1+1\right)^2}{\sqrt{x}+\sqrt{y}+\sqrt{z}}=\frac{9}{\sqrt{x}+\sqrt{y}+\sqrt{z}}\ge\frac{9}{x+y+z}=\frac{9}{3}=3\)
Dấu "=" xảy ra <=> x=y=z=1
Cho x, y là các số thực dương thỏa mãn điều kiện
5
x
+
2
y
+
3
3
x
y
+
x
+
1
5
x
y
5
+...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + y ( x - 2 ) .Tính giá trị nhỏ nhất của biểu thức T = x + y
![]()
![]()
![]()
![]()
Đáp án B.
Từ giả thiết, suy ra
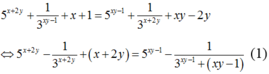
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 - ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f ( t ) luôn đồng biến trên ℝ .
Suy ra
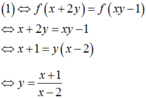
Do y > 0 nên x + 1 x - 2 > 0 ⇔ [ x > 2 x < - 1 . Mà x > 0 nên x > 2 .
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm
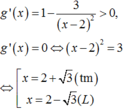
Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy min g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và x = 1 + 3 .
Đúng 0
Bình luận (0)
Cho x, y là các số thực dương thỏa mãn điều kiện
5
x
+
2
y
+
3
3
x
y
+
x
+
1
5
x
y
5
+
3
-...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + y ( x - 2 ) .
Tính giá trị nhỏ nhất của biểu thức T = x + y .
![]()
![]()
![]()
![]()
Tìm giá trị nhỏ nhất của biểu thức P = \(x^3+y^3+2x^2y^2\) biết rằng x và y là các số thực thỏa mãn điều kiện: x + y = 1
\(P=\left(x+y\right)^3-3xy\left(x+y\right)+2x^2y^2\)
\(=2x^2y^2-3xy+1=2t^2-3t+\frac{5}{8}+\frac{3}{8}\) (đặt t = xy \(\Rightarrow t\le\frac{\left(x+y\right)^2}{4}=\frac{1}{4}\))
\(=\frac{1}{8}\left(4t-1\right)\left(4t-5\right)+\frac{3}{8}\ge\frac{3}{8}\)
Do đó \(P\ge\frac{3}{8}\)
Đẳng thức xảy ra khi \(\hept{\begin{cases}x+y=1\\t=\frac{1}{4}\\x=y\end{cases}}\Leftrightarrow x=y=\frac{1}{2}\)
True?
Đúng 0
Bình luận (0)
Em không hiểu ctv giải dòng suy ra T ạ
๖ۣۜBFK_Quân Nguyễn~ đó là BĐT phụ nhé bạn:
\(xy\le\frac{\left(x+y\right)^2}{4}\Leftrightarrow4xy\le\left(x+y\right)^2\Leftrightarrow\left(x-y\right)^2\ge0\) ( đúng )
Đó,mình chứng minh đó nhé !
Xem thêm câu trả lời
Cho x, y là các số thực dương thỏa mãn điều kiện
5
x
+
2
y
+
3
3
x
y
+
x
+
1
5
x
y
5
+
3
−...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 − x − 2 y + y x − 2 . Tính giá trị nhỏ nhất của biểu thức T=x+y
A. T min = 2 + 3 2
B. T min = 3 + 2 3
C. T min = 3 2
D. T min = 5 + 3 2