Cho △ABC. Điểm I là điểm sao cho khoảng cách từ nó đến các đường thẳng AB, BC, AC bằng nhau. Hỏi có bao nhiêu điểm I thỏa mãn điều kiện đề bài?

Những câu hỏi liên quan
Cho △ABC. Điểm I là điểm sao cho khoảng cách từ nó đến các đường thẳng AB, BC, AC bằng nhau. Hỏi có bao nhiêu điểm I thỏa mãn điều kiện đề bài?
Gọi I là điểm thỏa mãn
IM; IN; IP lần lượt là khoảng cách từ I đến BC; AB; AC => IM = IN = IP
+) Dễ có tam giác vuông IMB = tam giác vuông INB (cạnh huyền- cạnh góc vuông)
=> góc IBN = IBM (2 góc tương ứng)
=> BI là p/ g của của góc ABC
+) Tương tự, AI là p/g của góc BAC ; CI là p/g của góc ACB
Vậy I là giao điểm của đường phân giác Của 3 góc của tam giác ABC
- Giả sử, còn điểm I' (khác I) thỏa mãn I'M = I'N = I'P
=> I' thuộc đường phân giác của góc ABC và góc BAC
Theo trên I là giao của 2 đường phân giác của góc ABC và góc BAC
=> I' trùng I (Vì hai đường thẳng phân biệt cắt nhau tại duy nhất 1 điểm)
Vậy Điểm I là duy nhất
Đúng 0
Bình luận (0)
1 điểm ! lần sau các bạn trả lời các câu hỏi của các bạn khác thì các bạn hãy xem các bạn đó có hơn 20 cup ko nhé . ko thì các bạn ấy tick ko đúng đấy
Đúng 0
Bình luận (0)
Cho tam giác ABC. Hãy tìm điểm sao cho khoảng cách từ điểm đó đến các đường thẳng AB, BC, AC bằng nhau và khoảng cách này là ngắn nhất.
Cho mặt phẳng tọa độ Oxy . Tam giác ABC nội tiếp đường tròn tâm I(—2;1) thỏa mãn điều kiện : góc AyB =90° . Chân đường cao kẻ từ A đến BC là D(—1;—1), đường thẳng AC đi qua điểm M(—1;4). Tìm tọa độ các đỉnh A, B biết điểm A có hoành độ dương.
Cho tam giác ABC vuông tại A. Vẽ các nửa đtròn đường kính AB, AC sao cho các nửa đtròn này không có điểm nào nằm trong tam giác ABC. Đương thẳng d qua A cắt nửa đtròn đường kính AB AC tại M,N. gọi I là trung điểm của BC.1. chứng minh BMNC là hình thang vuông2.cm IMIN3.giả sử đường thẳng d thay đổi nhưng vẫn thỏa mãn điều kiện đề bài. hãy xác định vị trí của đường thẳng d để chu vi tứ giác BMNC lớ nhấtgợi ý e câu 3 với ạ. em cảm ơn.
Đọc tiếp
Cho tam giác ABC vuông tại A. Vẽ các nửa đtròn đường kính AB, AC sao cho các nửa đtròn này không có điểm nào nằm trong tam giác ABC. Đương thẳng d qua A cắt nửa đtròn đường kính AB AC tại M,N. gọi I là trung điểm của BC.
1. chứng minh BMNC là hình thang vuông
2.cm IM=IN
3.giả sử đường thẳng d thay đổi nhưng vẫn thỏa mãn điều kiện đề bài. hãy xác định vị trí của đường thẳng d để chu vi tứ giác BMNC lớ nhất
gợi ý e câu 3 với ạ. em cảm ơn.
I. Trắc nghiệm ( 6 điểm)
Cho mặt cầu S(O; R) và đường thẳng Δ. Biết khoảng cách từ O tới Δ bằng d. Đường thẳng Δ tiếp xúc với S(O; R) khi thỏa mãn điều kiện nào trong các điều kiện sau ?
A. d = R
B. d > R
C. d < R
D. d ≠ R
Chọn A.
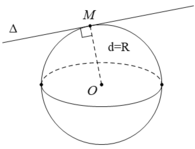
Đường thẳng Δ tiếp xúc với S( O; R) khi d = R.
Đúng 0
Bình luận (0)
Cho tam giác ABC. Hãy tìm một điểm sao cho khoảng cách từ điểm đó đến mỗi đường thẳng AB, BC, CA là bằng nhau, đồng thời khoảng cách này là ngắn nhất.
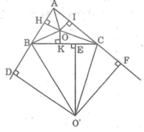
* Nếu O là điểm nằm trong ΔABC
Kẻ OH ⊥ AB, OK ⊥ BC, OI ⊥ AC
Vì điểm O cách đều các đường thẳng AB, BC, CA nên: OH = OK = OI
+) Ta có: OH = OK nên O nằm trên đường phân giác của góc ∠ABC.
Do OK = OI nên O nằm trên đường phân giác của góc ∠ACB
Do OH = OI nên O nằm trên đường phân giác của góc ∠BAC
Vậy O là giao điểm các đường phân giác trong của ΔABC
* Nếu O' nằm ngoài ΔABC
Kẻ O'D ⊥ AB, O'E ⊥ BC, O'F ⊥ AC
Vì O' cách đều ba đường thẳng AB, BC, AC nên: O'D = O'E = O'F
Vì O'D = O'F nên O' nằm trên tia phân giác của ∠(BAC)
Vì O'D = O'E nên O' nằm trên tia phân giác của ∠(DBC)
Suy ra O' là giao điểm phân giác trong của ∠(BAC) và phân giác ngoài tại đỉnh B.
Khi đó A, O, O' thẳng hàng ( vì hai tia AO và AO’ đều là tia phân giác của góc BAC) và A, H, D thẳng hàng
Ta có: OH < O'D
Vậy O là giao điểm các đường phân giác trong ΔABC cách đều ba đường thẳng AB, BC, CA và ngắn nhất.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;0;0), B(-2;0;3), M(0;0;1) và N(0;3;1). Mặt phẳng (P) đi qua các điểm M, N sao cho khoảng cách từ điểm B đến (P) gấp hai lần khoảng cách từ điểm A đến (P). Có bao nhiêu mặt phẳng (P) thỏa mãn đề bài? A. Chỉ có một mặt phẳng (P). B. Không có mặt phẳng (P) nào C. Có hai mặt phẳng (P). D. Có vô số mặt phẳng (P).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;0;0), B(-2;0;3), M(0;0;1) và N(0;3;1). Mặt phẳng (P) đi qua các điểm M, N sao cho khoảng cách từ điểm B đến (P) gấp hai lần khoảng cách từ điểm A đến (P). Có bao nhiêu mặt phẳng (P) thỏa mãn đề bài?
A. Chỉ có một mặt phẳng (P).
B. Không có mặt phẳng (P) nào
C. Có hai mặt phẳng (P).
D. Có vô số mặt phẳng (P).
Chọn đáp án D
Giả sử mặt phẳng (P) có vectơ pháp tuyến là n ⇀ = a ; b ; c a 2 + b 2 + c 2 ≠ 0 .
Khi đó phương trình mặt phẳng (P) có dạng a x + b y + c z + d = 0 .
Do M 0 ; 0 ; 1 ∈ P nên c + d = 0 ⇔ d = - c
Do N 0 ; 3 ; 1 ∈ P nên 3 b + c + d = 0 ⇔ b = 0
Khi đó P : a x + c z - c = 0
Từ giả thiết ta có d B ; P = 2 d A ; P
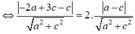
⇔ - 2 a + 2 c a 2 + c 2 = 2 a - c a 2 + c 2 (luôn đúng). Vậy có vô số mặt phẳng (P) thỏa mãn.
Đúng 0
Bình luận (0)
Cho tam giác ABC. Hãy tìm một điểm sao cho khoảng cách từ điểm đó đến mỗi đường thẳng AB, BC, CA là bằng nhau, đồng thời khoảng cách này là ngắn nhất ?
Điểm cách đều các đường thẳng AB và AC nằm trên các đường phân giác (trong và ngoài) của góc B.
Điểm cách đều các đường thẳng AB và AC nằm trên các đường phân giác (trong và ngoài) của góc A.
Điểm cách đều các đường thẳng AB, BC, CA là giao điểm của các đường phân giác trên, đó là bốn điểm I, K, M, N.
Để khoảng cách nói trên là ngắn nhất, ta chọn điểm I, giao điểm của các đường phân giác trong của \(\Delta ABC.\)
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB=AC). Hai đường trung trực của hai cạnh AB và AC cắt nhau tại O
a, CMR: khoảng cách từ điểm O đến cạnh BC bằng khoảng cách từ điểm O đến cạnh AC
b, Gọi I là một điểm nằm trên cạnh AB và K là một điểm nằm trên cạnh AC sao cho AI=AK. Tính số đo góc IOK biết rằng góc BAC = 30 độ











