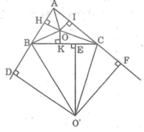
* Nếu O là điểm nằm trong ΔABC
Kẻ OH ⊥ AB, OK ⊥ BC, OI ⊥ AC
Vì điểm O cách đều các đường thẳng AB, BC, CA nên: OH = OK = OI
+) Ta có: OH = OK nên O nằm trên đường phân giác của góc ∠ABC.
Do OK = OI nên O nằm trên đường phân giác của góc ∠ACB
Do OH = OI nên O nằm trên đường phân giác của góc ∠BAC
Vậy O là giao điểm các đường phân giác trong của ΔABC
* Nếu O' nằm ngoài ΔABC
Kẻ O'D ⊥ AB, O'E ⊥ BC, O'F ⊥ AC
Vì O' cách đều ba đường thẳng AB, BC, AC nên: O'D = O'E = O'F
Vì O'D = O'F nên O' nằm trên tia phân giác của ∠(BAC)
Vì O'D = O'E nên O' nằm trên tia phân giác của ∠(DBC)
Suy ra O' là giao điểm phân giác trong của ∠(BAC) và phân giác ngoài tại đỉnh B.
Khi đó A, O, O' thẳng hàng ( vì hai tia AO và AO’ đều là tia phân giác của góc BAC) và A, H, D thẳng hàng
Ta có: OH < O'D
Vậy O là giao điểm các đường phân giác trong ΔABC cách đều ba đường thẳng AB, BC, CA và ngắn nhất.