a, xét tam giác EBC và tam giác DAC có : 

góc C chung

góc ADC = góc BEC = 90

=> tam giác EBC ~ tam giác DAC (g - g)

từ đề suy ra:

\(\widehat{BAC}=\widehat{DAC}.2=30^o.2=60^o\)

\(\widehat{ABC}=2.\widehat{EBC}=2.30^o=60^o\)

áp dụng đl tổng 3 góc trong của một tam giác :

\(\widehat{ACB}+\widehat{BAC}+\widehat{ABC}=180^o\)

\(\widehat{ACB}+60^o+60^o=180^o\)

\(\Rightarrow\widehat{ACB}=60^o\)

Xét tam giác ABC có 3 góc trong đều bằng nhau và bằng 60\(^o\)

suy ra : ABC là tam giác đều(đpcm)

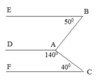
D A B ^ = 360 0 − 140 0 + 90 0 = 130 0

 a)  D A C ^   +   A C F ^ = 140 0 + 40 0 = 180 0

Suy ra AD//CF( vì có cặp góc trong cùng phía bù nhau).

b)  D A B ^   +   A B E ^ = 130 0 + 50 0 = 180 0

Suy ra AD//BE( vì có cặp góc trong cùng phía bù nhau)

a,Xét tam giác DAC và tam giác EBC ta có:

\(\widehat{BEC}=\widehat{ADC}=90^0\)

C chung 

 tam giác DAC đồng dạng  tam giác EBC

b, AD là đường cao vừa là đường phân giác 

BD = DC

DC = \(\dfrac{BC}{2}\) =\(\dfrac{6}{3}=2\)

Vì  tam giác DAC đồng dạng  tam giác EBC suy ra \(\dfrac{AC}{BC}=\dfrac{DC}{EC}\Leftrightarrow EC=\dfrac{DC.BC}{AC}=\dfrac{3.6}{9}=2\)

c, vì đường cao BE,CF nên \(\widehat{BEC}=\widehat{CFB}=90^o\)

Xét tam giác BEC và tam giác CFB có 

BC chung

\(\widehat{CBA}=\widehat{BCA}\)

tam giác BEC = tam giác CFB ( cạnh huyền góc nhọn )

CE = BF ( đpcm )

Ta có : AB = AC , CE = BF 

AB = BF + AF  ;    AC = CE + AE 

suy ra AF = AE     => tam giác AEF cân tại A

\(\widehat{ÀEF}=\dfrac{180^o-\widehat{A}}{2}\)   ( 1 )

tam giác ABC cân tại A suy ra \(\widehat{ACB}=\dfrac{180^o-\widehat{A}}{2}\)  ( 2 )

TỪ ( 1 ) và ( 2 ) ta có \(\widehat{AEF}=\widehat{ACB}\) 

suy ra  EF//BC ( có cặp góc đồng vị bằng nhau )

a) Xét ΔDAC vuông tại D và ΔEBC vuông tại E có

\(\widehat{ECB}\) chung

Do đó: ΔDAC∼ΔEBC(g-g)

thong cam e k bt

a. Gọi giao điểm của AK và BN là Q

Ta có: 

ˆDMB+ˆMBD=90∘DMB^+MBD^=90∘

Mà ˆAME+ˆMAE=90∘AME^+MAE^=90∘

ˆAME=ˆDMBAME^=DMB^ (2 góc đối đỉnh)

⇒ˆMBD=ˆMAE⇒ˆQAM=ˆMBD⇒MBD^=MAE^⇒QAM^=MBD^

Mà ˆAMN=ˆDMBAMN^=DMB^ (2 góc đối đỉnh)

⇒ˆAMN+ˆQAM=ˆDMB+ˆMBD=90∘⇒AMN^+QAM^=DMB^+MBD^=90∘

⇒ˆAQM=90∘⇒AQM^=90∘

Hay AK vuông góc với BN.

b. Theo câu a: AK vuông góc với BN tại Q

Mà BQ là phân giác của góc ˆIBKIBK^ 

Khi đó: tam giác IBK có đường cao là đường phân giác nên tam giác IBK cân tại B

Vậy BQ cũng là trung tuyến hay Q là trung điểm của IK.

Chứng minh tương tự: Q là trung điểm của MN

Xét tứ giác MINK có 2 đường chéo giao nhau tại trung điểm mỗi đường, MN vuông góc với IK

Vậy MINK là hình thoi.