Phương trình (m-5)x+m2-25=0 có vô số nghiệm . Khi đó, m=...

Những câu hỏi liên quan
tìm m để phương trình (m+1)x2 + 2(m+3)x - m+2 =0 có 2 nghiệm phân biệt
tìm các giá trị của tham số m để bất phương trình (m2 - 4m -5)x2 +2(m-5)x-1\(\ge0\) vô nghiệm
a.
Pt có 2 nghiệm pb khi:
\(\left\{{}\begin{matrix}m+1\ne0\\\Delta'=\left(m+3\right)^2-\left(m+1\right)\left(-m+2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\2m^2+7m+7>0\left(\text{luôn đúng}\right)\end{matrix}\right.\)
\(\Rightarrow m\ne-1\)
b.
BPT vô nghiệm khi \(\left(m^2-4m-5\right)x^2+2\left(m-5\right)-1< 0\) nghiệm đúng với mọi x
- Với \(m=-1\) ko thỏa mãn
- Với \(m=5\) thỏa mãn
- Với \(m\ne\left\{-1;5\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}m^2-4m-5< 0\\\Delta'=\left(m-5\right)^2+m^2-4m-5< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\\left(m-5\right)\left(2m-4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\2< m< 5\end{matrix}\right.\) \(\Rightarrow2< m< 5\)
Kết hợp lại ta được: \(2< m\le5\)
Đúng 0
Bình luận (0)
Bài 4:
a) Tìm m để phương trình sau có nghiệm duy nhất: 2x - mx + 2m - 1 = 0.
b) Tìm m để phương trình sau có vô số nghiệm: mx + 4 = 2x + m2.
c) Tìm m để phương trình sau có nghiệm duy nhất dương: (m2 - 4)x + m - 2 = 0
à bài này a nhớ (hay mất điểm ở bài này) ;v
Đúng 2
Bình luận (2)
xinloi cậu tớ muốn giúp lắm mà tớ ngu toán:)
Đúng 0
Bình luận (7)
a)Ta có \(2x-mx+2m-1=0\\ =>x\left(2-m\right)+2m-1=0\)
Để pt có nghiệm duy nhất thì \(a\ne0=>2-m\ne0\\=>m\ne2\)
b)Ta có \(mx+4=2x+m^2\\ =>mx+4-2x+m^2=0\\ =>\left(m-2\right)x=m^2-4\)
Để pt vô số nghiệm thì \(\left\{{}\begin{matrix}m-2=0\\m^2-4=0\end{matrix}\right.=>\left\{{}\begin{matrix}m=2\\m=\pm2\end{matrix}\right.\)\(=>m=2\)
c)Để pt có nghiệm duy nhất thì \(m^2-4\ne0>m\ne\pm2\)
Chắc vậy :v
Đúng 2
Bình luận (0)
Cho phương trình m 2 + 5 m + 4 x 2 = m + 4 , trong đó m là một số. Chứng minh rằng: Khi m = - l, phương trình nghiệm vô nghiệm.
Thay m = - l vào vế trái phương trình :
- 1 2 + 5 - 1 + 4 x 2 = 0 x 2
Vế phải phương trình : - l + 4 = 3
Phương trình đã cho trở thành : 0 x 2 = 3 không có giá trị nào của x thỏa mãn phương trình. Vậy phương trình vô nghiệm.
Đúng 0
Bình luận (0)
a Tìm m để phương trình vô nghiệm: x2 - (2m - 3)x + m2 = 0.
b Tìm m để phương trình vô nghiệm: (m - 1)x2 - 2mx + m -2 = 0.
c Tìm m để phương trình vô nghiệm: (2 - m)x2 - 2(m + 1)x + 4 - m = 0
\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)
Đúng 0
Bình luận (0)
Giá trị của tham số m để phương trình ( 3 - m ) x - m 2 + 9 = 0 có vô số nghiệm là:
![]()
B. m > 3.
C. m < 3.
D. m = 3.
Đáp án: D
Để phương trình (3 – m )x – m 2 + 9 = 0 có vô số nghiệm thì
3 - m = 0 m 2 - 9 = 0 ⇔ m = 3
Đúng 0
Bình luận (0)
Cho phương trình
(
m
2
+
1
)
(
x
2
-
3
x
+
2
)
2011
-
3
x
+
4
0Các phát biểu :(1) Phương trình trên vô nghiệm vơi mọi m(2) Khi m 1 phương trình trên có nghiệm(3) Không tồn tại m để phương trình trên vô nghiệmChọn đáp án đúng: A. (1) đúng B. (2),(3) Đúng C. A, B đ...
Đọc tiếp
Cho phương trình ( m 2 + 1 ) ( x 2 - 3 x + 2 ) 2011 - 3 x + 4 = 0
Các phát biểu :
(1) Phương trình trên vô nghiệm vơi mọi m
(2) Khi m = 1 phương trình trên có nghiệm
(3) Không tồn tại m để phương trình trên vô nghiệm
Chọn đáp án đúng:
A. (1) đúng
B. (2),(3) Đúng
C. A, B đều đúng
D. Tất cả đều sai.
Cho phương trình (ẩn x) x2 – 2(m – 1)x + m2 = 0
Với giá trị nào của m thì phương trình có hai nghiệm phân biệt? Có nghiệm kép? Vô nghiệm.
Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > 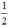
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m = 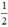
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m < 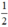
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < 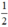 ; có nghiệm kép khi m =
; có nghiệm kép khi m = 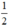 và vô nghiệm khi m >
và vô nghiệm khi m > 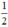
Đúng 0
Bình luận (0)
Cho phương trình: (4
m
2
– 9)x 2
m
2
+ m – 3. Tìm m để phương trình có vô số nghiệm A. m
-
3
2
B. m 1 C. m
3
2
D. m
2
3
Đọc tiếp
Cho phương trình: (4 m 2 – 9)x = 2 m 2 + m – 3. Tìm m để phương trình có vô số nghiệm
A. m = - 3 2
B. m = 1
C. m = 3 2
D. m = 2 3
Cho phương trình m 2 + 5 m + 4 x 2 = m + 4 , trong đó m là một số. Chứng minh rằng: Khi m = - 2 hoặc m = -3, phương trình vô nghiệm.
Thay m = - 2 vào vế trái phương trình :
- 2 2 + 5 - 2 + 4 x 2 = - 2 x 2
Vế phải phương trình: - 2 + 4 = 2
Phương trình đã cho trở thành: - 2 x 2 = 2 không có giả trị nào của x thỏa mãn vì vế trái âm mà vế phải dương. Vậy phương trình vô nghiệm.
Thay m = - 3 vào về trái phương trình:
- 3 2 + 5 - 3 + 4 x 2 = - 2 x 2
Vế phải phương trình : - 3 + 4 = l
Phương trình đã cho trở thành : - 2 x 2 = 1 không có giả trị nào của x thỏa mãn vì vế trái là số âm mà vế phải là số dương. Vậy phương trình vô nghiệm.
Đúng 0
Bình luận (0)















