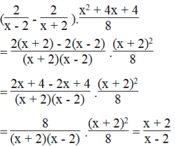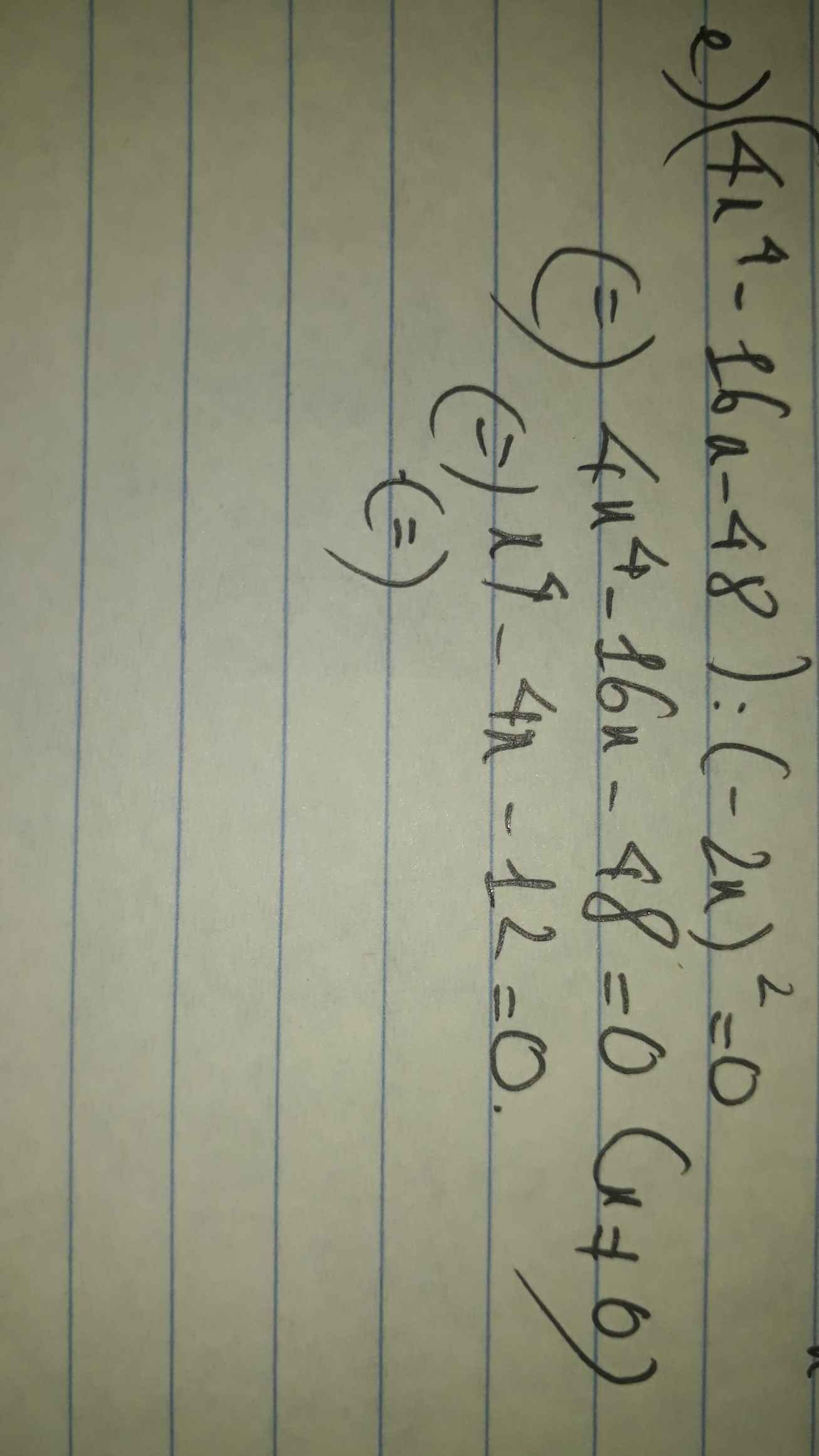\(2^{2x}+2^{2x+1}=48\)

\(2^{2x}+2^{2x}.2=48\)

\(2^{2x}.\left(1+2\right)=48\)

\(2^{2x}.3=48\)

\(2^{2x}=48:3\)

\(2^{2x}=16\)

\(2^{2x}=2^4\)

\(\Rightarrow2x=4\)

\(x=4:2\)

\(x=2\)

\(2^{2x}+2^{2x+1}=48\\ \Rightarrow2^{2x}+2.2^{2x}=48\\ \Rightarrow\left(1+2\right).2^{2x}=48\\ \Leftrightarrow3.2^{2x}=48\\ \Leftrightarrow2^{2x}=16\\ \Leftrightarrow2^{2x}=2^4\\ \Leftrightarrow2x=4\\ \Leftrightarrow x=2\)

Vậy x = 2

x = 2 

(2x² + 1)(x-3)=0

\(\Rightarrow\orbr{\begin{cases}2x^2+1=0\\x-3=0\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}2x^2=-1\Rightarrow x^2=-\frac{1}{2}\left(vl\right)\\x=3\end{cases}}\)

Vậy x=3

48-(15-x)⁵=48

     (15-x)⁵=48-48

     (15-x)⁵=0

=>  15-x   =0

           x    =15-0

           x    =15

Vậy x=15

a: Ta có: \(x\left(2-x\right)+\left(x^2+x\right)=7\)

\(\Leftrightarrow2x-x^2+x^2+x=7\)

\(\Leftrightarrow3x=7\)

hay \(x=\dfrac{7}{3}\)

b: Ta có: \(\left(2x+1\right)^2-x\left(4-5x\right)=17\)

\(\Leftrightarrow4x^2+4x+1-4x+5x^2=17\)

\(\Leftrightarrow9x^2=16\)

\(\Leftrightarrow x^2=\dfrac{16}{9}\)

hay \(x\in\left\{\dfrac{4}{3};-\dfrac{4}{3}\right\}\)

c: Ta có: \(\left(x-4\right)^2-\left(2x+1\right)^2=0\)

\(\Leftrightarrow\left(x-4-2x-1\right)\left(x-4+2x+1\right)=0\)

\(\Leftrightarrow\left(x+5\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=1\end{matrix}\right.\)

d: ta có: \(\dfrac{2x^3-8x^2+10x}{2x}=0\)

\(\Leftrightarrow x^2-4x+5=0\)

\(\Leftrightarrow\left(x-2\right)^2+1=0\)(vô lý)

a: Ta có: \(x\left(2-x\right)+x^2+x=7\)

\(\Leftrightarrow2x-x^2+x^2+x=7\)

\(\Leftrightarrow3x=7\)

hay \(x=\dfrac{7}{3}\)

b: Ta có: \(\left(x-4\right)^2-\left(2x+1\right)^2=0\)

\(\Leftrightarrow\left(x-4-2x-1\right)\left(x-4+2x+1\right)=0\)

\(\Leftrightarrow\left(x+5\right)\left(3x-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=1\end{matrix}\right.\)

1) \(x^2+x-6=x\left(x-2\right)+3\left(x-2\right)=\left(x+3\right)\left(x-2\right)\)

2) \(x^2-x-6=\left(x-3\right)\left(x+2\right)\)

3) \(x^2+2x-48=\left(x-6\right)\left(x+8\right)\)

4) \(x^2-2x-48=\left(x-8\right)\left(x+6\right)\)

5) \(x^2+x-42=\left(x-6\right)\left(x+7\right)\)

6) \(x^2-x-42=\left(x-7\right)\left(x+6\right).\)

bài này tìm x hay tìm cực trị vậy

1) \(x^2+x-6\)

\(=x^2-2x+3x-6\)

\(=\left(x^2-2x\right)+\left(3x-6\right)\)

\(=x\left(x-2\right)+3\left(x-2\right)\)

\(=\left(x-2\right)\left(x+3\right)\)

2) \(x^2-x-6\)

\(=x^2+2x-3x-6\)

\(=\left(x^2+2x\right)-\left(3x+6\right)\)

\(=x\left(x+2\right)-3\left(x+2\right)\)

\(=\left(x+2\right)\left(x-3\right)\)

3) \(x^2+2x-48\)

\(=x^2+8x-6x-48\)

\(=\left(x^2+8x\right)-\left(6x+48\right)\)

\(=x\left(x+8\right)-6\left(x+8\right)\)

\(=\left(x+8\right)\left(x-6\right)\)

4) \(x^2-2x-48\)

\(=x^2-8x+6x-48\)

\(=\left(x^2-8x\right)+\left(6x-48\right)\)

​\(=x\left(x-8\right)+6\left(x-8\right)\)​

\(=\left(x-8\right)\left(x+6\right)\)

5) \(x^2+x-42\)

\(=x^2+7x-6x-42\)

\(=\left(x^2+7x\right)-\left(6x+42\right)\)

\(=x\left(x+7\right)-6\left(x+7\right)\)

\(=\left(x+7\right)\left(x-6\right)\)

6) \(x^2-x-42\)

\(=x^2-7x+6x-42\)

\(=\left(x^2-7x\right)+\left(6x-42\right)\)

\(=x\left(x-7\right)+6\left(x-7\right)\)

\(=\left(x-7\right)\left(x+6\right)\)

\(x=3y=2z\)

\(\Rightarrow\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\)

\(\Rightarrow\frac{2x}{2}=\frac{3y}{6}=\frac{4z}{12}=\frac{2x-3y+4z}{2-6+12}=\frac{48}{8}=6\)

Rồi thế vào là ra thôi :

 \(\frac{2x}{2}=6\Rightarrow x=..........\)

Rồi tương tự thôi

6)

\(x=3y=2z\)

\(\Rightarrow\frac{x}{6}=\frac{y}{2}=\frac{z}{3}\)

\(\Rightarrow\frac{2x}{12}=\frac{3y}{6}=\frac{4z}{12}\)

Áp dụng tc của dãy tỉ số bằng nhau ta có

\(\frac{2x}{12}=\frac{3y}{6}=\frac{4z}{12}=\frac{2x-3y+4z}{12-6+12}=\frac{48}{18}=\frac{24}{9}\)

\(\Rightarrow\begin{cases}x=16\\y=\frac{16}{3}\\z=8\end{cases}\)

7)

\(2x=3y=-2z\)

\(\Rightarrow\frac{2x}{1}=\frac{3y}{1}=\frac{-4z}{2}\)

Áp dụng tc của dãy tỉ số bằng nhau ta có

\(\frac{2x}{1}=\frac{3y}{1}=\frac{-4z}{2}=\frac{2x-3y-\left(-4z\right)}{1-1-2}=\frac{48}{-2}=-24\)

\(\Rightarrow\begin{cases}x=-12\\y=-8\\z=12\end{cases}\)

6) *2x - 3y + 4z = 48

<=> 4z -2z +4z = 48

=> ( 4-2+4)z = 48

=> z=8  => 2z= 16

* 2x -3y + 4z =48

<=> 6y - 3y +6y =48

=> (6 - 3+ 6)y = 48

=> y= \(\frac{16}{3}\) => 3y = 16

* 2x - 3y + 4z =48

<=> 2x -x + 2x = 48

=> ( 2 -1 +2)x =48

=>x= 16

Ta có: 2x³ + 3x² - 32x =48

<=>    2x³  + 3x² - 32x - 48 =0

<=>   x²(2x+3) - 16(2x+3)   =0

<=>   (x²-16)(2x+3)             =0

<=>   (x-4)(x+4)(2x+3)        =0

<=>  x-4=0 hoặc x+4=0 hoặc 2x+3=0

<=>  x=4 hoặc x=-4 hoặc x= \(\dfrac{-3}{2}\)

Vậy phương trình trên có tập nghiệm là S={4;-4;\(\dfrac{-3}{2}\)}

2x³+3x²-32x=48

⇔2x³+3x²-32x-48=0

⇔x²(2x+3)-16(2x+3)=0

⇔(2x+3)(x²-16)=0

⇔(2x+3)(x-4)(x+4)=0

⇔2x+3=0 hoặc x-4=0 hoặc x+4=0

1.2x+3=0⇔2x=-3⇔x=-3/2

2.x-4=0⇔x=4

3.x+4=0⇔x=-4

phương trình có 3 nghiệm:x=-3/2 và x=4 và x=-4

Ta có: \(2x^3+3x^2-32x=48\)

\(\Leftrightarrow2x^3+3x^2-32x-48=0\)

\(\Leftrightarrow x^2\left(2x+3\right)-16\left(2x+3\right)=0\)

\(\Leftrightarrow\left(2x+3\right)\left(x^2-16\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+3=0\\x^2-16=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-3\\x^2=16\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=4\\x=-4\end{matrix}\right.\)

vậy: \(S=\left\{-\dfrac{3}{2};4;-4\right\}\)