Cho các điểm A(2;-3) B(3;7) C(6;1)
a, Viết phương trình đường tròn (C) ngoại tiếp tam giác ABC
b, Viết phương trình đường tròn (C') nội tiếp tam giác ABC
c, Tìm M ϵ (C), N ϵ (C') sao cho độ dài MN ngắn nhất
Những câu hỏi liên quan
Cho các điểm sau: A(–2; –3); B(–2; 3); C(4; 3); M(2; 6); N(–2; 2); P(2; –2).
a) Biểu diễn các điểm đã cho trên mặt phẳng tọa độ.
b) Tìm tọa độ điểm D; Q sao cho ABCD và MNPQ là hình vuông.
Cho các điểm sau: A(–2; –3); B(–2; 3); C(4; 3); M(2; 6); N(–2; 2); P(2; –2).
a) Biểu diễn các điểm đã cho trên mặt phẳng tọa độ.
b) Tìm tọa độ điểm D; Q sao cho ABCD và MNPQ là hình vuông.
Cho các điểm sau: A(–2; –3); B(–2; 3); C(4; 3); M(2; 6); N(–2; 2); P(2; –2).
a) Biểu diễn các điểm đã cho trên mặt phẳng tọa độ.
b) Tìm tọa độ điểm D; Q sao cho ABCD và MNPQ là hình vuông.
Cho 3 điểm A,B,C thẳng hàng sao cho A và C nằm khác phía đối với điểm B và 1 điểm M nằm bên ngoài đường thẳng chứa 3 điểm A,B,C. a)Vẽ tất cả các đường thẳng đi qua 2 điểm trong các điểm đã cho b)Kể tên các đường thẳng có trong hình vẽ
1. Cho AB2 ,I là trung điểm AB. Tìm tập hợp các điểm M sao cho MA^2-MB^282. Trg mp vs hệ tọa độ Oxy , cho 2 điểm A(1;-2) và B (2;3). Gọi M (a;0) là điểm sao cho tứ giác OABM là hình thang . Tìm a3. Tìm tất cả các gtri của m để pt sqrt{2x^2-x-2m}m-2 có nghiệm 4. Tìm tất cả giá trị của m để pt x^2-2x-3-m0 có nghiệm xin[0;4]Help me
Đọc tiếp
1. Cho AB=2 ,I là trung điểm AB. Tìm tập hợp các điểm M sao cho \(MA^2-MB^2=8\)
2. Trg mp vs hệ tọa độ Oxy , cho 2 điểm A(1;-2) và B (2;3). Gọi M (a;0) là điểm sao cho tứ giác OABM là hình thang . Tìm a
3. Tìm tất cả các gtri của m để pt \(\sqrt{2x^2-x-2m}=m-2\) có nghiệm
4. Tìm tất cả giá trị của m để pt \(x^2-2x-3-m=0\) có nghiệm \(x\in[0;4]\)
Help me
2)Vẽ 4 điểm A,B,M,N sao cho điểm A nằm giữa 2 điểm M và B;điểm N nằm giữa A và B
a)Hãy cho biết điểm A còn nằm giữa 2 điểm nào?
b)Tìm các điểm nằm khác phía và cùng phía đối với điểm A.
cho hai đường thẳng a//b. trên đường thẳng a có n điểm, trên đường thẳng b có m điểm ( m,n thuộc N, m>=2, n>=2)
a) có bao nhiêu tam giác mà đỉnh là các điểm đã cho?
b) có bao nhiêu hình thang mà đỉnh là các điểm đã cho?
Cho các điểm A(-1; 2), B(-2; 1), C(2; -3), D(2; 0), O(0; 0). Có bao nhiêu điểm nằm trong góc phần tư thứ 2 trong số các điểm trên?
A. 0
B. 1
C. 2
D. 3
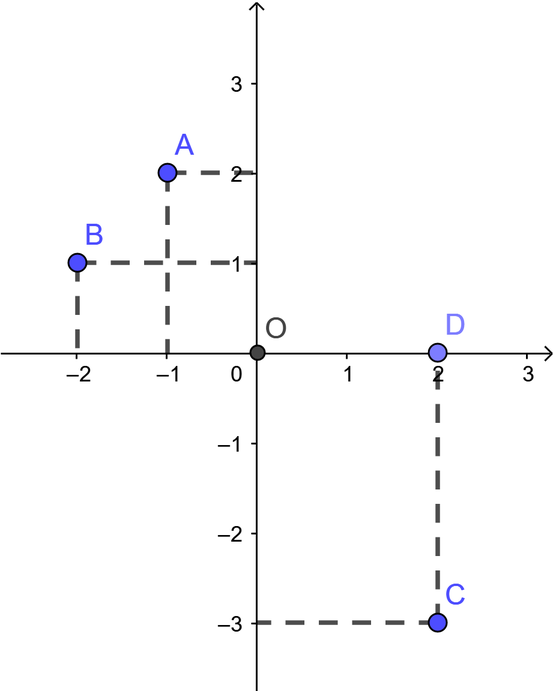
Biểu diễn các điểm trên hệ trục tọa độ Oxy ta thấy có hai điểm nằm trong góc phần tư thứ hai là A và B
Chọn đáp án C
Đúng 0
Bình luận (0)
Cho 99 điểm trên mặt phẳng trong đó có 2 điểm A, B cách nhau 3 cm. Mỗi nhóm 3 điểm bất kì của các điểm đã cho bao giờ cũng chọn ra được 2 điểm có khoảng cách nhỏ hơn 1 cm. Vẽ đường tròn (A;1cm) và (B;1cm). Chứng tỏ rằng trong hai đường tròn đã cho có một đường tròn chứa ít nhất 50 điểm trong số các điểm đã cho
Gọi C là điểm bất kì trong 97 điểm còn lại
Ba điểm A,B,C lập thành một nhóm.
Theo giả thiết một nhóm bao giờ cũng có thể chọn ra hai điểm có khoảng cách nhỏ hơn 1cm
Theo nguyên lí Điriclê thì phải có một đường tròn chứa ít nhất 49 điểm.
Thêm điểm A hoặc B nữa thì có một đường tròn chứa ít nhất 50 điểm.
Đúng 0
Bình luận (0)
Cho các điểm A (1; 2), B (-3; 1), C (4; 2), quỹ tích các điểm M thỏa mãn \(MA^2+MB^2=MC^2\) là đường tròn (C) tâm I, tung độ điểm I là ?
Gọi \(M\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(x-1;y-2\right)\\\overrightarrow{BM}=\left(x+3;y-1\right)\\\overrightarrow{CM}=\left(x-4;y-2\right)\end{matrix}\right.\)
\(MA^2+MB^2=MC^2\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y-2\right)^2+\left(x+3\right)^2+\left(y-1\right)^2=\left(x-4\right)^2+\left(y-2\right)^2\)
\(\Leftrightarrow x^2+y^2+12x-2y-5=0\)
\(\Rightarrow I\left(-6;1\right)\)
Đúng 1
Bình luận (0)