Cho tam giác ABC vuông tại A. Đường cao AH chia cạnh huyền thành hai đoạn: BH = 4cm; CH = 9cm. Gọi D, E theo thứ tự đó là chân đường vuông góc hạ từ H xuống AB và AC.
a) Tính độ dài đoạn thẳng DE?
b) Chứng minh đẳng thức AE.AC = AD.AB?
c) Gọi các đường tròn (O), (M), (N) theo thứ tự ngoại tiếp các tam giác ABC, DHB, EHC. Xác định vị trí tương đối giữa các đường tròn: (M) và (N); (M) và (O); (N) và (O)?
d) Chứng minh DE là tiếp tuyến chung của hai đường tròn (M) và (N) và là tiếp tuyến của đường tròn đường kính MN?

Những câu hỏi liên quan
Cho tam giác vuông ABC vuông tại A, chân đường cao AH của tam giác ABC chia cạnh huyền BC thành hai đoạn thẳng BH 4cm, HC 9cm. Tính diện tích tam giác ABC? A.
S
A
B
C
39
c
m
2
B.
S
A
B
C...
Đọc tiếp
Cho tam giác vuông ABC vuông tại A, chân đường cao AH của tam giác ABC chia cạnh huyền BC thành hai đoạn thẳng BH = 4cm, HC = 9cm. Tính diện tích tam giác ABC?
A. S A B C = 39 c m 2
B. S A B C = 36 c m 2
C. S A B C = 78 c m 2
D. S A B C = 19 c m 2
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A
Ta có: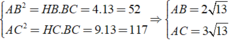
Vậy S A B C = 1 2 A B . A C = 1 2 . 2 13 . 3 13 = 39 c m 2
Chọn đáp án A.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành 2 đoạn: BH = 4 và HC = 6 cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành 2 đoạn: BH = 4 và HC = 6 a) tính độ dài AH, AB, AC b) Gọi M là trung điểm của AC. Tính số đo góc AMB ( làm tròn đến độ)
a: \(AH=2\sqrt{6}\left(cm\right)\)
\(AB=2\sqrt{10}\left(cm\right)\)
\(AC=2\sqrt{15}\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành 2 đoạn: BH = 4 và HC = 6
cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành 2 đoạn: BH = 4 và HC = 6
a) tính độ dài AH, AB, AC
b) Gọi M là trung điểm của AC. Tính số đo góc AMB ( làm tròn đến độ)
c) Kẻ AK vuông góc BM (K thuộc BM). Chứng mih : BK.BM=BH.BC
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AC^2=CH\cdot BC\\AB^2=BH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=2\sqrt{6}\left(cm\right)\\AC=2\sqrt{15}\left(cm\right)\\AB=2\sqrt{10}\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền thành hai đoạn thẳng có độ dài 4cm và 9cm. Diện tích tam giác vuông đó là: A. 39
c
m
2
B. 36
c
m
2
C. 18
c
m
2
D. 27
c
m
2
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền thành hai đoạn thẳng có độ dài 4cm và 9cm. Diện tích tam giác vuông đó là:
A. 39 c m 2
B. 36 c m 2
C. 18 c m 2
D. 27 c m 2
Cho tám giác ABC vuông tại A , đường cao AH chia cạnh huyền thành hai đoạn BH = 4cm và Hc = 9cm
a) tính AH,AB,AC
b) Từ H kẻ vuông góc với Ab , HF vuông góc với AC ( E thuộc AB , F thuộc AC). Chứng mình rằng AB.AE=AF.AC và tam giác AEF đồng dạng với tam giác AC
c)Gọi D là trung điểm BC. Chúng minh rằng 2.sin ²C+cos ADB=1
giúp em với ạ
b: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC. Tính độ dài đoạn thẳng DE
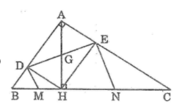
![]()
Tứ giác ADHE có 3 góc vuông nên nó là hình chữ nhật
Suy ra: AH = DE (tính chất hình chữ nhật)
Tam giác ABC vuông tại A và có AH là đường cao
Theo hệ thức giữa đường cao và hình chiếu ta có:
A H 2 = HB.HC = 4.9 = 36 ⇒ AH = 6 (cm)
Vậy DE = 6 (cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC. Tính diện tích tứ giác DENM
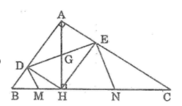
Tam giác BDH vuông tại D có DM là đường trung tuyến nên:

Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành hai đoạn ; BH=4cm và HC=6cm
a) Tính độ dài các đoạn AH,AB,AC
b) Gọi M là trung điểm của AC . Tính số đo góc AMB ( làm tròn đến độ )
c) Kẻ AK vuông góc với BM ( K thuộc BM ) . Chứng minh BK.BM=BH.BC
Cho tam giác ABC vuông tại A có AH là đường cao chia cạnh huyền BC thành hai đoạn BH=4cm; HC = 6cm
b) gọi M là chung điểm của AC. Tính số đo góc AMB( làm tròn đến độ)
c)kẻ AK vuông góc với BM (K thuộc BM) . Chứng minh BK.BM=BH.BC
c: Xét ΔABM vuông tại A có AK là đường cao
nên \(BK\cdot BM=AB^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BK\cdot BM=BH\cdot BC\)
Đúng 0
Bình luận (1)
cho tam giác ABC vuông tại A có AH là đường cao chia cạnh huyền BC thành hai đoạn BH=4cm; HC = 6cm
b) gọi M là chung điểm của AC. Tính số đo góc AMB( làm tròn đến độ)
c)kẻ AK vuông góc với BM (K thuộc BM) . Chứng minh BK.BM=BH.BC
c: Xét ΔABM vuông tại A có AK là đường cao ứng với cạnh huyền BM
nên \(BK\cdot BM=AB^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BK\cdot BM=BH\cdot BC\)
Đúng 1
Bình luận (0)














