chứng minh C=1+3+3^2+...+3^23 ko chia hết cho 3
cần gấp
ai đúng mik cho 5 điểm ạaaa
Bài 5: (1 điểm) Cho A= 2+22+23+24+.....+2100 . Chứng minh A chia hết cho 3.
Lời giải:
$A=(2+2^2)+(2^3+2^4)+....+(2^{99}+2^{100})$
$=2(1+2)+2^3(1+2)+...+2^{99}(1+2)$
$=2.3+2^3.3+...+2^{99}.3$
$=3(2+2^3+...+2^{99})\vdots 3$
Ta có đpcm.
1 . cho abc = 2deg
chứng minh abcdeg chia hết cho 23 , 29
2. cho abcd chia hết cho 101
chứng minh ab - cd = 0
3. chứng minh
a, 31993 - 2157 không chia hết cho 2
b, 24n + 2 + 1 chia hết cho 5
ai trả lời hết và đúng nhất sẽ nhanh được like
cho C=5+5mũ 2 + 5 mũ 3+.....+5 mũ 20
a)chứng minh c chia hết cho 5
b)chứng minh c chia hết cho 6
c)chứng minh c chia hết cho 1
bài 3
cho C=1+3+3 mũ 2 +...+3 mũ 11.Chứng minh C chia hết 40
Cho C=3-3^2+3^3-3^4+3^5-3^6+...+3^23-3^24. Chứng minh C chia hết cho 420
\(C=3-3^2+3^3-3^4+3^5-3^6+...-3^{22}+3^{23}-3^{24}\)
\(=\left(3-3^2+3^3\right)-\left(3^4-3^5+3^6\right)+...-\left(3^{22}-3^{23}+3^{24}\right)\)
\(=3\left(1-3+3^2\right)-3^4\left(1-3+3^2\right)+...-3^{22}\left(1-3+3^2\right)\)
\(=7\left(3-3^4+...-3^{22}\right)⋮7\)
\(C=3-3^2+3^3-3^4+3^5-3^6+...-3^{22}+3^{23}-3^{24}\)
\(=\left(3-3^2+3^3-3^4\right)+\left(3^5-3^6+3^7-3^8\right)+...+\left(3^{21}-3^{22}+3^{23}-3^{24}\right)\)
\(=3\left(1-3+3^2-3^3\right)+3^5\left(1-3+3^2-3^3\right)+...+3^{21}\left(1-3+3^2-3^3\right)\)
\(=-20\cdot\left(3+3^5+...+3^{21}\right)\)
\(=-60\cdot\left(1+3^4+...+3^{20}\right)⋮60\)
\(C⋮60;C⋮7\)
mà ƯCLN(60;7)=1
nên C chia hết cho 60*7=420
1) Cho A=4+4^2+2^4+...+2^20.Hỏi A có chia hết cho 128 ko ?
2) Cho S =5+5^2+5^3+...+5^2006.
a) Tính S
b) Chứng minh: S chia hết cho 126 .
4) Cho C =3+3^2+3^3+3^4+....+3^300.Chứng tỏ C chia hết cho 40
A ,chứng minh rằng nếu hai số tự nhiên cùng chia cho 5 và có cùng số dư thì hiệu của chúng chia hết cho 5
B,cho 2 số tự nhiên a và b ko chia hết cho 3 khi chia a avf b cho 3 thì có 2 số dư khác nhau chứng minh rằng ( a +b )chia hết cho 3
mik cần rất rất là gấp mong các bạn giúp mik tik
Hơi khó nha! @@@
â) Gọi số thứ nhất là x, số thứ 2 là y, thương của phép chia 1 là m, thương của phép chia 2 là n, số dư của 2 phép chia đó là a. Theo đề bài, ta có:
\(x:5=m\)(dư a)
\(y:5=n\)(dư a)
\(x-y⋮5\)
Ta có:
\(5.5=5+5+5+5+5\)
\(5.4=5+5+5+5\)
=> Khoảng cách giữa mỗi tích là 5.
Vậy tích 1 + 5 = tích 2
=> tích 1 (dư a) + 5 = tích 2 (dư a)
Mà:
5 = tích 2 (dư a) - tích 1 (dư a)
5 = tích 2 - tích 1 (a biến mất do a - a = 0 (Một số bất kì trừ chính nó = 0))
tích 2 - tích 1 = 5
Không có thời gian làm câu b sorry bạn nhé!
Mình sẽ làm sau!
1.Cho A =1+3+3^2+....+3^10
chứng tỏ rằng A chia hết cho 13 , A chia hết cho 40
2.Cho B=2.4.6.8.10.12+40
hỏi B có chia hết cho 6 ko
3.C= 23!+191-15!
chứng tỏ C chia hết cho 11
Bạn nào trả lời đúng mình sẽ kết bạn với bạn đó nha
\(1,A=1+3+3^2+...+3^{10}\)
\(A=1.\left(1+3+9\right)+...+3^6.\left(1+3+9\right)+3^{10}\)
Vì \(\hept{\begin{cases}1.\left(1+3+9+\right)+3^3.\left(1+3+9\right)+3^6.\left(1+3+9\right)⋮\\3^{10}⋮̸13\end{cases}13}\)
\(A⋮̸13\)
Cho A = 2 + 2 2 + 2 3 + . . . + 2 20 . Chứng minh rằng:
a) A chia hết cho 2;
b) A chia hết cho 3;
c) A chia hết cho 5.
a) A chia hết cho 2 vì tất cả các số hạng của tổng đều chia hết cho 2.
b) Ta tách ghép các số hạng của A thành các nhóm sao cho mỗi nhóm xuất hiện thừa số chia hết cho 3. Khi đó:

![]()
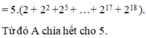
cho c = 2 + 2 mũ 3 + 2 mũ 5 + ....+ 2 mũ 23 chứng minh rằng
a, c chia hết cho 21 b, c chia hết cho 10
`#3107.101107`
a,
\(C=2+2^3+2^5+...+2^{23}\)
\(=\left(2+2^3+2^5\right)+\left(2^5+2^7+2^9\right)+...+\left(2^{19}+2^{21}+2^{23}\right)\)
\(=2\left(1+2^2+2^4\right)+2^5\cdot\left(1+2^2+2^4\right)+...+2^{19}\cdot\left(1+2^2+2^4\right)\)
\(=\left(1+2^2+2^4\right)\cdot\left(2+2^5+...+2^{19}\right)\)
\(=21\cdot\left(2+2^5+...+2^{19}\right)\)
Vì \(21\text{ }⋮\text{ }21\)
\(\Rightarrow21\left(2+2^5+...+2^{19}\right)\text{ }⋮\text{ }21\)
Vậy, \(C\text{ }⋮\text{ }21\)
b,
\(C=2+2^3+2^5+...+2^{23}\)
\(=\left(2+2^3\right)+\left(2^5+2^7\right)+...+\left(2^{21}+2^{23}\right)\)
\(=\left(2+2^3\right)+2^4\cdot\left(2+2^3\right)+...+2^{20}\cdot\left(2+2^3\right)\)
\(=\left(2+2^3\right)\cdot\left(1+2^4+...+2^{20}\right)\)
\(=10\cdot\left(1+2^4+...+2^{20}\right)\)
Vì \(10\text{ }⋮\text{ }10\)
\(\Rightarrow10\cdot\left(1+2^4+...+2^{20}\right)\text{ }⋮\text{ }10\)
Vậy, \(C\text{ }⋮\text{ }10.\)
a) c = 2 + 2³ + 2⁵ + ... + 2¹⁹ + 2²¹ + 2²³
= (2 + 2³ + 2⁵) + (2⁷ + 2⁹ + 2¹¹) + ... + (2¹⁹ + 2²¹ + 2²³)
= 2.(1 + 2² + 2⁴) + 2⁷.(1 + 2² + 2⁴) + ... + 2¹⁹.(1 + 2² + 2⁴)
= 2.21 + 2⁷.21 + ... + 2¹⁹.21
= 21.(2 + 2⁷ + ... + 2¹⁹) ⋮ 21
Vậy c ⋮ 21
b) c = 2 + 2³ + 2⁵ + 2⁷ + ... + 2²¹ + 2²³
= (2 + 2³) + (2⁵ + 2⁷) + ... + (2²¹ + 2²³)
= 10 + 2⁴.(2 + 2³) + ... + 2²⁰.(2 + 2³)
= 10 + 2⁴.10 + ... + 2²⁰.10
= 10.(1 + 2⁴ + ... + 2²⁰) ⋮ 10
Vậy c ⋮ 10
Bài 1 chứng Minh
a,N^2+n+6 ko chia hết cho 5
b,n^2+n+1 ko chia hết cho4
c,n ( n + 1 ) ( n + 5 ) chia hết cho 3
ử dụng phương pháp phản chứng
giả sử n chia hết cho 5
=>n có dạng 5k
=>n^2+n+1=25k^2+5k+1=5k(5k+1)+1
ta có 5k(5k+1) chia hết cho 5 mà 1 ko chia hết cho 5
=>25k^2+5k+1 ko chia hết cho 5 (đpcm)