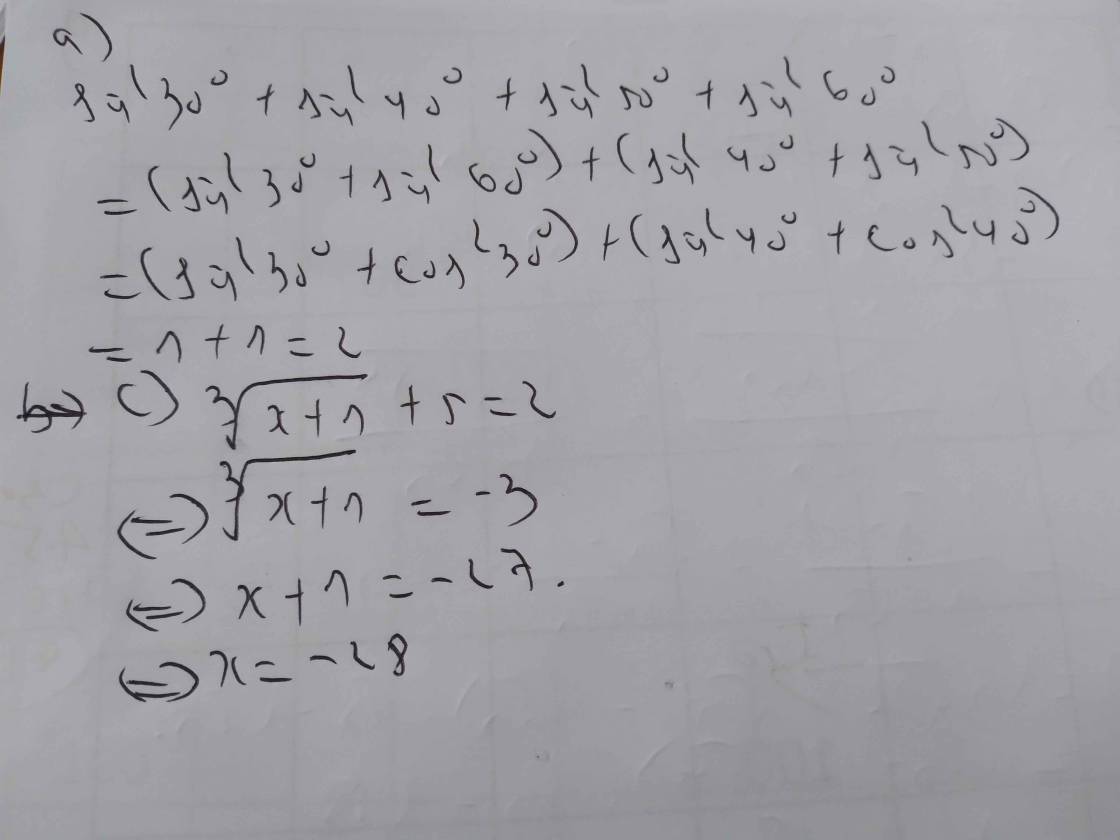\(=\dfrac{tan\left(\dfrac{pi}{2}+x\right)\cdot sin\left(-x\right)\cdot cos\left(x-pi\right)}{cos\left(\dfrac{pi}{2}-x\right)\cdot sin\left(x+pi\right)}\)

\(=\dfrac{-cotx\cdot sin\left(-x\right)\cdot\left(-cosx\right)}{sinx\cdot-sinx}\)

\(=\dfrac{cotx\cdot sinx\left(-1\right)\cdot cosx}{-sinx\cdot sinx}=\dfrac{\dfrac{cosx}{sinx}\cdot cosx}{sinx}=\dfrac{cos^2x}{sin^2x}=cot^2x\)

a: \(\sin36^0-\cos54^0+\cos60^0\)

\(=\sin36^0-\sin36^0+\dfrac{1}{2}=\dfrac{1}{2}\)

b: \(=\left(\sin^210^0+\sin^280^0\right)+\left(\sin^230^0+\sin^260^0\right)\)

=1+1=2

`sin36^o -cos54^o +cos60^o`

`=cos54^o -cos54^o +cos60^o`

`=cos60^o=1/2`

_____________________________________________

`sin^2 10^o +sin^2 30^o +sin^2 80^o +sin^2 60^o`

`=cos^2 80^o +cos^2 60^o +sin^2 80^o +sin^2 60^o`

`=(cos^2 80^2 +sin^2 80^o )+(cos^2 60^o +sin^2 60^o )`

`=1+1=2`

\(A=sin^210+sin^220+sin^230+sin^280+sin^270+sin^260=sin^210+sin^220+sin^230+cos^210+cos^220+cos^230=1+1+1=3\)\(B=\left(1+tan^2\alpha\right)\left(1-sin^2\alpha\right)+\left(1+cot^2\alpha\right)\left(1-cos^2\alpha\right)=\dfrac{1}{cos^2\alpha}.cos^2\alpha+\dfrac{1}{sin^2\alpha}.sin^2\alpha=1+1=2\)

\(P=sin^22x-\left[2sin\dfrac{x}{2}cos\dfrac{x}{2}\left(cos^4\dfrac{x}{2}-sin^4\dfrac{x}{2}\right)\right]^2\)

\(=sin^22x-\left[sinx\left(cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}\right)\left(cos^2\dfrac{x}{2}+sin^2\dfrac{x}{2}\right)\right]^2\)

\(=sin^22x-\left[sinx.cosx.1\right]^2\)

\(=sin^22x-\left[\dfrac{1}{2}sin2x\right]^2\)

\(=\dfrac{3}{4}sin^22x=\dfrac{3}{4}\left(1-cos^22x\right)=\dfrac{3}{4}\left(1-\dfrac{1}{4}\right)=\dfrac{9}{16}\)

1: \(P=sin^22x=1-cos^22x\)

\(=1-\left(cos2x\right)^2\)

\(=1-\left(2cos^2x-1\right)^2\)

\(=1-\left(2\cdot\dfrac{9}{16}-1\right)^2\)

\(=1-\left(\dfrac{9}{8}-1\right)^2=1-\left(\dfrac{1}{8}\right)^2=\dfrac{63}{64}\)

2:

\(cos2x-sin\left(x+\dfrac{\Omega}{3}\right)=0\)

=>\(sin\left(x+\dfrac{\Omega}{3}\right)=cos2x=sin\left(\dfrac{\Omega}{2}-2x\right)\)

=>\(\left[{}\begin{matrix}x+\dfrac{\Omega}{3}=\dfrac{\Omega}{2}-2x+k2\Omega\\x+\dfrac{\Omega}{3}=\Omega-\dfrac{\Omega}{2}+2x+k2\Omega\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}3x=\dfrac{\Omega}{6}+k2\Omega\\-x=\dfrac{1}{6}\Omega+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Omega}{18}+\dfrac{k2\Omega}{3}\\x=-\dfrac{1}{6}\Omega-k2\Omega\end{matrix}\right.\)

B

B

Lời giải:

$\sin ^230^0+\sin ^260^0=\sin ^230^0+cos ^2(90^0-60^0)$

$=\sin ^230^0+\cos ^230^0=1$

Đáp án B.

\(S=sinx+siny+sin\left(3x+y\right)-sin\left(3x+y\right)-sin\left(x+y\right)\)

\(=sinx+siny-sin\left(x+y\right)\)

\(S^2=\left(sinx+siny-sin\left(x+y\right)\right)^2\le3\left(sin^2x+sin^2y+sin^2\left(x+y\right)\right)\)

\(S^2\le3\left(1-\dfrac{1}{2}\left(cos2x+cos2y\right)+sin^2\left(x+y\right)\right)\)

\(S^2\le3\left[1-cos\left(x+y\right)cos\left(x-y\right)+1-cos^2\left(x-y\right)\right]\)

\(S^2\le3\left[2+\dfrac{1}{4}cos^2\left(x+y\right)-\left[cos\left(x-y\right)-\dfrac{1}{2}cos\left(x+y\right)\right]^2\right]\le3\left[2+\dfrac{1}{4}cos^2\left(x+y\right)\right]\)

\(S^2\le3\left(2+\dfrac{1}{4}\right)=\dfrac{27}{4}\)

\(\Rightarrow S\le\dfrac{3\sqrt{3}}{2}\)

\(\Rightarrow\left\{{}\begin{matrix}a=3\\b=3\\c=2\end{matrix}\right.\)

\(\left(\sqrt{\dfrac{1+sin\alpha}{1-sin\alpha}}+\sqrt{\dfrac{1-sin\alpha}{1+sin\alpha}}\right).\dfrac{1}{\sqrt{1+tan^2\alpha}}\)

\(=\left(\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{\left(1+sin\alpha\right)\left(1-sin\alpha\right)}}\right).\dfrac{1}{\sqrt{1+\left(\dfrac{sin\alpha}{cos\alpha}\right)^2}}\)

\(=\left(\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{1-sin^2\alpha}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{1-sin^2\alpha}}\right).\dfrac{1}{\sqrt{\dfrac{cos^2\alpha+sin^2\alpha}{cos^2\alpha}}}\)

\(=\left(\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{cos^2\alpha}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{cos^2\alpha}}\right).\dfrac{1}{\sqrt{\dfrac{1}{cos^2\alpha}}}\)

\(=\left(\dfrac{1+sin\alpha}{cos\alpha}+\dfrac{1-sin\alpha}{cos\alpha}\right).\dfrac{1}{\dfrac{1}{cos\alpha}}=\dfrac{2}{cos\alpha}.cos\alpha=2\)