vì góc A bằng 90 độ nên:

 góc B + góc C = 180-90=90 độ

\(\Rightarrow\)góc BIC = 180 - (90 : 2) = 135 độ

a/

+ Xét tam giác ABC có

^A = 180 -B - C =70 <=> 35 = 90 - B/2 -C/2 <=> 35 + 90 = 90 + 90 - B/2 - C/2 <=> 125 = 180 - B/2 - C/2

+ Xét tam giác BIC

BIC = 180 - IBC - ICB = 180 - B/2 - C/2 => BIC = 125

b/ Kéo dài BC về phía c tạo thành tia Bx theo đề bài BI kéo dài cắt tia phân giác của góc ACx tại K ta có

C + ACx = 180 => ICA + ACK = C/2 + ACx/2 = ICK = 180/2 = 90

Xét tam giác ICK có BKC = 180 - KIC - ICK

Mà KIC = 180 - BIC = 180 - 125 = 55

=> BCK = 180 - 55 - 90 = 35

ai bit giup mình với nha thanks

Mik cần gấp ai làm được thì mik cảm ơn nhiều nhé.

\(a,\widehat{BIC}=180^0-\widehat{IBC}-\widehat{ICB}=180^0-\dfrac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)=180^0-\dfrac{1}{2}\left(180^0-\widehat{BAC}\right)=180^0-\dfrac{1}{2}\cdot100^0=130^0\)

a: \(\widehat{BIC}=180^0-\dfrac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)\)

\(=180^0-\dfrac{1}{2}\cdot100^0=130^0\)

Vì tam giác ABC là tam giác cân tại A nên B=C

Mà A=70 nên B+C=110

Suy ra B=C=110/2=55

Lại có B1=B2=55/2=27,5

góc C t/ư

Xét tam giác BICcos:

B2+BIC +C2=180(ĐL tổng 3 góc trong tam giác)

27,5+BIC+27,5=180

BIC=180-27,5-27,5

BIC=55

Vậy ...

a/ Xét tg BIC có

\(\widehat{BIC}=180^o-\left(\widehat{IBC}+\widehat{ICB}\right)=180^o-\dfrac{\widehat{B}}{2}-\dfrac{\widehat{C}}{2}=\)

\(=180^o-\left(\dfrac{\widehat{B}+\widehat{C}}{2}\right)=180^o-\left[\dfrac{180^o-\widehat{A}}{2}\right]=90^o+\dfrac{\widehat{A}}{2}\left(dpcm\right)\)

b/ Để c/m câu này ta chứng minh bài toán phụ: " Hai đường phân giác ngoài của 2 góc với đường phân giác trong của góc còn lại đồng quy"

Có hai đường phân giác của các góc ngoài của góc B và góc C cắt nhau tại J.

Từ J dựng các đường vuông góc với AB; AC; BC cắt 3 cạnh trên lần lượt tại D; E; F 

Vì J thuộc đường phân giác của \(\widehat{DBC}\) nên JD=JF

Vì J thuộc đường phân giác của \(\widehat{ECB}\) nên JE=JF

(Mọi điểm thuộc đường phân giác của một góc thì cách đều hai cạnh của góc)

=> JD=JE

Xét tg vuông ADJ và tg vuông AEJ có

ẠJ chung; JD=JE (cmt) => tg ADJ = tg AEJ (hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)

\(\Rightarrow\widehat{DAJ}=\widehat{EAJ}\) => Ạ là phân giác của góc \(\widehat{BAC}\)

Áp dụng vào bài toán:

Nối AJ => AJ là phân giác của \(\widehat{BAC}\) => AJ phải đi qua I (Trong tg 3 đường phân giác trong đồng quy) => A; I; J thẳng hàng

c/ Vì J; H; K bình đẳng nên B; I; K thẳng hàng và C; I; H thẳng hàng

=> AJ; BK; CH đồng quy tại I

+)Xét tam giác ABC có góc A +ABC+ACB=180 độ(định lí tổng 3 góc trong một tam giác )

mà A=80 độ (gt)

suy ra ABC+ACB=180-80=100(1)

+)Có BI là phân giác ABC(gt)

suy ra góc CBI=IBA=ABC/2(tính chất ..)

+)CMTT có BIC=ICA=ACB/2

SUY RA góc IBC+ICB=ABC+ACB/2

MÀ có (1)suy ra IBC+ICB=50(2)

+)Xét tam giác BIC có(2)nên suy ra BIC=180-50=130

NẾU MUỐN MK LÀM NỐT THÌ KẾT BẠN VỚI MÌNH NHÉ!!!!Thank you for watching!!

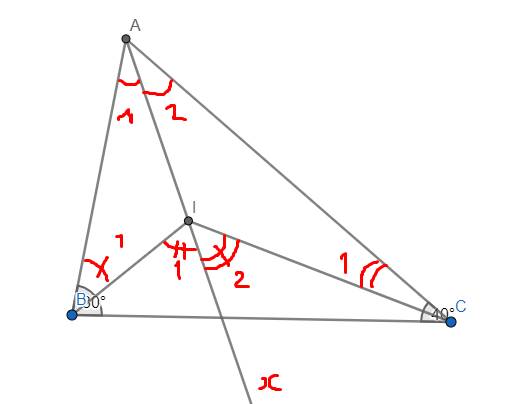
Ta có \(\widehat{I_1}=\widehat{A_1}+\widehat{B_1}\) và \(\widehat{I_2}=\widehat{A_2}+\widehat{C_1}\)

\(\Rightarrow\widehat{BIC}=\widehat{I_1}+\widehat{I_2}\)

\(=\left(\widehat{A_1}+\widehat{A_2}\right)+\left(\widehat{B_1}+\widehat{C_1}\right)\)

\(=\widehat{BAC}+\dfrac{\widehat{ABC}+\widehat{ACB}}{2}\)

\(=180^o-\left(\widehat{ABC}+\widehat{ACB}\right)+\dfrac{\widehat{ABC}+\widehat{ACB}}{2}\)

\(=180^o-\left(80^o+40^o\right)+\dfrac{80^o+40^o}{2}\)

\(=120^o\)

Vậy \(\widehat{BIC}=120^o\)

B1: Cho tam giác ABC có B=80, C=40 độ. Tia phân giác của góc B cắt AC tại D. Tính ADB.

B2:  Cho ta giác ABC có B-C=20 độ. Đường phân giác AD của góc A cắt BC tại D. Tính ADB  và  ADC.

B3: Cho hình vẽ tính ACB