viết phương trình đường thẳng d trong các trường hợp sau 1. d đi qua M (4;3) và có hệ số góc 1/4 2 d đi qua N (- căn 3 ; 4) và tạo với tia ox 1 góc 30 độ

Những câu hỏi liên quan
Viết phương trình tham số, phương trình chính tắc của đường thẳng ∆ trong các trường hợp sau: ∆ đi qua hai điểm C(1; -1; 1) và D(2; 1; 4)
∆ đi qua hai điểm C và D nên có vecto chỉ phương CD → = (1; 2; 3)
Vậy phương trình tham số của ∆ là
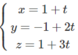
Phương trình chính tắc của ∆ là:
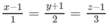
Đúng 0
Bình luận (0)
Viết phương trình tham số của đường thẳng d trong mỗi trường hợp sau: d đi qua M(5; 4; 1) và có vectơ chỉ phương a → = 2 ; - 3 ; 1
Cho A(1;-1) , B(3;0) , Δ:x-2y-4=0. Viết phương trình đường thẳng d trong các trường hợp sau :a, d đi qua A và vuông góc với ABb, d là đường trung trực của ABc, d đi qua B và song song với Δd, d đi qua A và B
Δ có vecto pháp tuyến là \(\overrightarrow{n}\) = (1; - 2) và vectochỉ phương
là \(\overrightarrow{u}\) = (2; 1)
a, d ⊥ AB nên d nhận \(\overrightarrow{AB}=\left(2;1\right)\) làm vecto pháp tuyến
Phương trình đường thẳng d: 2(x - 1) + (y + 1) = 0
hay 2x + y - 1 = 0
b, Trung điểm M của AB : \(M\left(2;-\dfrac{1}{2}\right)\)
d ⊥ AB nên d nhận \(\overrightarrow{AB}=\left(2;1\right)\) làm vecto pháp tuyến
Phương trình đường thẳng d: 2(x - 2) + \(\left(y+\dfrac{1}{2}\right)\) = 0
hay 2x + y \(-\dfrac{7}{2}\) = 0
c, d // Δ nên vecto pháp tuyến của Δ là vecto pháp tuyến của d ⇒ d nhận \(\overrightarrow{n}\) = (1; - 2) làm vecto pháp tuyến
d đi qua B (3; 0)
Phương trình d: 1(x-3) - 2y = 0 hay x - 2y - 3 = 0
d, d đi qua A và B thì d nhận \(\overrightarrow{AB}=\left(2;1\right)\) làm vecto chỉ phương ⇒ d nhận (1; -2) làm vecto pháp tuyến
phương trình d: x - 2y - 3 = 0
Đúng 0
Bình luận (0)
Viết phương trình tham số của đường thẳng d trong mỗi trường hợp sau: d đi qua hai điểm P(1; 2; 3) và Q(5; 4; 4).
vecto chỉ phương của d là a = PQ = (4;2;1) (vì d đi qua hai điểm P(1;2;3),Q(5;4;4)
Vậy pt tham số của đường thẳng d là: x = 1 + 4 t y = 2 + 2 t z = 3 + t
Đúng 0
Bình luận (0)
viết phương trình đường thẳng d trong các trường hợp sau:
a) d đi qua điểm A nằm trên Ox có hoành độ bằng -3 và song song với đường thẳng d1 : y=-5x+4
b) d vuông góc với đường thẳng d2 : y=-1/2x +2018 và đi qua giao điểm của d3 : y=-x+3
Viết phương trình tham số của đường thẳng d trong mỗi trường hợp sau: d đi qua B(2; 0; -3) và song song với đường thẳng
∆
:
x
1
+
2
t
y
-
3
+...
Đọc tiếp
Viết phương trình tham số của đường thẳng d trong mỗi trường hợp sau: d đi qua B(2; 0; -3) và song song với đường thẳng ∆ : x = 1 + 2 t y = - 3 + 3 t z = 4 t
Vecto chỉ phương của đường thẳng d là a = (2;3;4) (vì d// ∆ )
Vậy pt tham số của đường thẳng d là: x = 2 + 2 t y = - 3 t z = - 3 + 4 t
Đúng 0
Bình luận (0)
Viết phương trình đường thẳng d đi qua hai điểm A, B trong các trường hợp sau
a) A ( 0;4) , B (-3;0)
b A( 0;3) , B (0;-2)
Xem chi tiết
Ta có :
\(\overrightarrow{AB}\) = (-3;-4)
\(\Rightarrow\overrightarrow{n}=\left(4;-3\right)\) là vectơ pháp tuyến của đường thẳng AB
Vậy phương trình đường thẳng AB là :
4x - 3(y-4) = 0
hay 4x - 3y = -4
Câu b tương tự
Đúng 2
Bình luận (0)
viết phương trình đường thẳng Δ trong các trường hợp sau:
a) đi qua A(3;2) ; B(-1;-5) ; M(-3;1) ; N(1;-6)
b) đi qua A(3;-1) và song song d: 2x+3y-1=0
c) đi qua M(3;2) và vecto n=(2;2)
d) đi qua A(1;1) và có hệ số góc k=2
Viết phương trình tham số của đường thẳng d trong mỗi trường hợp sau: d đi qua A(2; -1; 3) và vuông góc với mặt phẳng (α): x + y – z + 5 = 0.
Đường thẳng d vuông góc với mp α x+y-z+5=0 nên đường thẳng d có vecto chỉ phương n → = 1 ; 1 ; - 1
Vậy pt tham số của đường thẳng d là: x = 2 + t y = - 1 + t z = 3 - t
Đúng 0
Bình luận (0)
Lập phương trình tham số của đường thẳng d trong mỗi trường hợp sau:
a)d đi qua điểm M(2;1)và có vecto chỉ phương u
→=(3;4)
b)d đi qua điểm M(-2;3)và có vecto chỉ phương n
→=(5;1)















