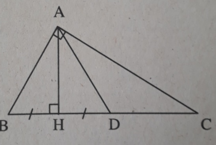
Trên HC lấy D sao cho HD = HB. Tam giác ABD có đường cao AH là trung tuyến nên là tam giác cân, suy ra

∠(ADB) = ∠B . (1)

Ta có: DC = HC – HD = HC – HB = AB = AD ( vì tam giác ABD cân tại A)

Nên ΔADC cân tại D, do đó ∠(DAC) = ∠C (2)

Ta có; ∠ADB + ∠DAC = ∠BAC = 90º (3)

Và ∠B + ∠C = 90º vì tam giác ABC vuông tại A (4)

Từ (2); (3) và (4) suy ra ∠(DAB) = ∠B . (5)

Từ (1) và (5) suy ra ∠(ADB) = ∠B = ∠(DAB) , do đó ΔABD là tam giác đều.

Suy ra AB = BD = AD = DC. Vậy BC = 2AB.

Do HC -HB = AB

Mà HC +HB =BC =>  nhân 2 vế ta có:

HC² -HB² =AB.BC (1).

Áp dụng định lí Pi-ta-go ta có:

HC² =AC²-AH²

HB² = AB² -AH² 

Nên HC² - HB² =AC² -AB² = (BC² -AB² ) -AB² = BC² -2AB² ,(2).

Từ (1 ) và (2 ) có: BC² - 2AB² =AB.BC

                          <=> BC² -AB.BC - 2AB² = 0

                           <=> (BC +AB) (BC -2AB ) = 0,

Do AB +BC >0 nên BC = 2AB.

HC -HB = AB, HC +HB =BC 
nhân 2 vế ta có HC^2 -HB^2 =AB.BC (1). 
Áp dụng Pitago ta có HC ^2 =AC^2-AH^2, HB^2 = AB^2 -AH^2 nên HC^2 - HB^2 =AC^2 -AB^2 = (BC^2 -AB^2 ) -AB^2 = BC^2 -2AB^2 ,(2). Từ (1 ) và (2 ) có BC^2 - 2AB^2 =AB.BC 
<=> BC^2 -AB.BC - 2AB^2 = 0 
<=> (BC +AB) (BC -2AB ) = 0, 
do AB +BC >0 => BC - 2AB = 0 => BC = 2AB.

:3

HC -HB = AB, HC +HB =BC 
Nhân 2 vế ta có HC^2 -HB^2 =AB.BC (1). 

Áp dụng Pitago ta có:

HC² = AC² - AH²; HB² = AB² nên:

HC² - HB² = AC² - AB² = (BC² - AB²) - AB² = BC² - 2AB²

Từ (1) có BC² - 2AB² = AB . BC

<=> BC² - AB . BC - 2AB² = 0

<=> (BC + AB)(BC - 2AB ) = 0, 
Do AB +BC > 0 => BC - 2AB = 0 => BC = 2AB.

help me

a)Áp dụng định lí Py-ta-go vào tam giác AHB ta được:

HB²+HA²=AB² 

\(\Rightarrow\) 3²+4²=AB²

\(\Rightarrow\) 9+16 =AB²

\(\Rightarrow\)\(\sqrt{AB}\) =25

\(\Rightarrow\)AB =5

b) tam giác AKH có AI vuông góc với KH(gt) , IH=IK(gt)

\(\Rightarrow\) AI vừa là đường cao vừa là đường trung tuyến

\(\Rightarrow\) tam giác AKH cân tại A

a) Xét ΔABH vuông tại H và ΔACH vuông tại H có AB=AC(ΔABC cân tại A)

AH chung

Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)