Question

Tam giác ABC vuông tại A, đường cao AH, HC – HB = AB. Chứng minh rằng BC = 2AB.

Answer 1

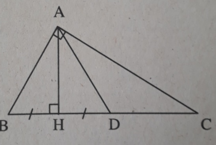
Trên HC lấy D sao cho HD = HB. Tam giác ABD có đường cao AH là trung tuyến nên là tam giác cân, suy ra

∠(ADB) = ∠B . (1)

Ta có: DC = HC – HD = HC – HB = AB = AD ( vì tam giác ABD cân tại A)

Nên ΔADC cân tại D, do đó ∠(DAC) = ∠C (2)

Ta có; ∠ADB + ∠DAC = ∠BAC = 90º (3)

Và ∠B + ∠C = 90º vì tam giác ABC vuông tại A (4)

Từ (2); (3) và (4) suy ra ∠(DAB) = ∠B . (5)

Từ (1) và (5) suy ra ∠(ADB) = ∠B = ∠(DAB) , do đó ΔABD là tam giác đều.

Suy ra AB = BD = AD = DC. Vậy BC = 2AB.