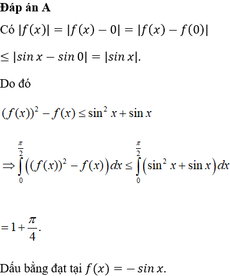Cho f(x)=\(\text{ax}+b\)thoả mãn f(f(f(0)))=2 và f(f(f(1)))=29. Khi đó giá trị của a là:

Những câu hỏi liên quan
Cho hàm số f(x)=ax+b thỏa mãn đẳng thức
f(f(f(0)))=2 và f(f(f(1)))=29
Khi đó giá trị của a là bao nhiêu?
cho hàm số f(x)= ax+b thỏa mãn các đẳng thức f(f(f(0)))=2 và f(f(f(1)))=29.Khi đó giá trị của a là?
A-1
B-3
C-4
D-5
1,Tìm các hệ số AB của đa thức f(x) = ax + b, biết : f(1)=1; f(2)=4
2, cho đa thứcf(x) : ax mũ 2 + bx + c = 0 ( vs mọi giá trị x ) . CMR : a=b=c=0
3, Cho đa thức f(x) thỏa mãn, f(x) + x. f(-x) = x+1 vs mọi giá trị của x. Tính f(1)
cho hàm số y=f(x)=ax-2 có đồ thị đi qua A( a+1,a2+a).
a, Tìm a
b, với giá trị a tìm được giá trị x thoả mãn f(2x-1)=f(1-2x)
Cho hàm số f (x) có đạo hàm cấp hai liên tục trên đoạn [0;1] thoả mãn
[
f
(
x
)
]
2
+
f
(
x
)
f
(
x
)
≥
1
,
∀
x
∈
[
0
;
1
]
và
f
2
(
0
)
+
f
(...
Đọc tiếp
Cho hàm số f (x) có đạo hàm cấp hai liên tục trên đoạn [0;1] thoả mãn [ f ' ( x ) ] 2 + f ( x ) f '' ( x ) ≥ 1 , ∀ x ∈ [ 0 ; 1 ] và f 2 ( 0 ) + f ( 0 ) . f ' ( 0 ) = 3 2 . Giá trị nhỏ nhất của tích phân ∫ 0 1 f 2 ( x ) d x bằng
A. 5 2
B. 1 2
C. 11 6
D. 7 2
Cho hàm số yf(x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;3] thoả mãn f(0)3, f(3)8 và
∫
0
3
(
f
(
x
)
)
2
f
(
x
)
+...
Đọc tiếp
Cho hàm số y=f(x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;3] thoả mãn f(0)=3, f(3)=8 và ∫ 0 3 ( f ' ( x ) ) 2 f ( x ) + 1 d x = 4 3 Giá trị của f(2) bằng
A. 64 9
B. 55 9
C. 16 3
D. 19 3
Cho hàm số f(x) = ax+b, biết f(-2) = -1 và f(3) = 9. khi đó giá trị của f(1) =
Cho hàm số f(x) liên tục trên R thoả mãn f(0)0 và
|
f
(
x
)
-
f
(
y
)
|
≤
|
sin
x
-
sin
y
|
với mọi
x
,
y
∈
R
. Giá trị lớn nhất của tích phân
∫
0
π
2
(
(
f
(
x...
Đọc tiếp
Cho hàm số f(x) liên tục trên R thoả mãn f(0)=0 và | f ( x ) - f ( y ) | ≤ | sin x - sin y | với mọi x , y ∈ R . Giá trị lớn nhất của tích phân ∫ 0 π 2 ( ( f ( x ) ) 2 - f ( x ) ) d x bằng
A. π 4 +1
B. π 8
C. 3 π 8
D. 1- π 4
Cho hàm số f(x) thỏa mãn
f
x
a
x
+
b
x
2
,
f
x
a...
Đọc tiếp
Cho hàm số f(x) thỏa mãn f ' ' x = a x + b x 2 , f x = a x 2 2 - b x + c và f - 1 = 2 , f 1 = 4 , f ' 1 = 0 . Tính giá trị của T =abc
A. T = 5 2
B. T = - 5 2
C. T = 1
D. T = - 1
Chọn đáp án B
Từ giả thiết, ta có hệ phương trình
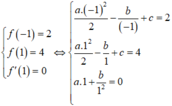
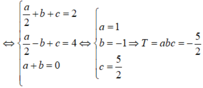
Đúng 0
Bình luận (0)