Cho tam giác ABC có\(_{\widehat{ }C}\)=60 ,\(\widehat{A}=2\widehat{B}\)
So sánh 3 cạnh tam giác
Những câu hỏi liên quan
24 tháng 1 2022 lúc 21:38
Cho tam giác ABC có \(\widehat{A}\)= 60o; \(\widehat{B}\)= 80o và có phân giác AD
a) So sánh các cạnh của tam giác ADC
b) So sánh các cạnh của tam giác ADB
thôi nha mik tự làm đc r
Cho hai tam giác ABC và A’B’C’ (Hình 57) có: \(\widehat A = \widehat {A'} = 60^\circ \), AB = A’B’ = 3 cm, \(\widehat B = \widehat {B'} = 45^\circ \). Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
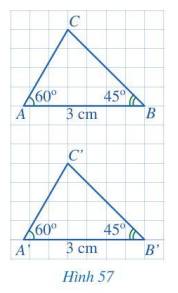
BC = B’C’ = 4 (đường chéo của 4 ô vuông).
Tam giác ABC và tam giác A’B’C’ có: BC = B’C’, AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(c.g.c)
Đúng 0
Bình luận (0)
Cho tam giác ABC có: \(\widehat A = 42^\circ ,\widehat B = 37^\circ \).
a) Tính \(\widehat C\).
b) So sánh độ dài các cạnh AB, BC, CA.
a) Trong tam giác ABC: \(\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 42^\circ - 37^\circ = 101^\circ \).
b) Trong tam giác ABC: \(\widehat B < \widehat A < \widehat C\)nên \(AC < BC < AB\). (Vì AC đối diện với góc B; BC đối diện với góc A; AB đối diện với góc C).
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(\widehat{A}\)= 70 độ, \(\widehat{B}\): \(\widehat{C}\)= 2 : 3. So sánh các cạnh của tam giác ABC
#GIÚPMKNHA
Xét tam giác ABC có : A + B + C = 180 độ
mà A = 70 độ => B + C = 110 độ
B : C = 2 : 3 => B/2 = C/3
=> B/2 = C/3 = B + C / 2 + 3 ( áp dụng t.c dãy tỉ số bằng nhau )
=> B/2 = C/3 = 110/5
=> B/2 = C/3 = 22
=> B = 22 . 2 = 44 ( độ )
C = 22 . 3 = 66 ( độ )
Do 44 độ < 66 độ < 70 độ
=> B < C < A
=> AC < AB < BC ( quan hệ cạnh đối diện và góc lớn hơn )
TK mk nha !!!
Đúng 0
Bình luận (0)
a) So sánh các góc của tam giác ABC có AB = 4 cm, BC = 7 cm, AC = 6 cm.
b) So sánh các cạnh của tam giác ABC có \(\widehat A\)\( = {50^o}\),\(\widehat C\)\( = {50^o}\)
a) Theo đề bài ta có AB = 4cm, BC = 7cm, AC = 6cm
Có góc đối diện với cạnh AB là góc C, góc A đối diện với cạnh BC, góc B đối diện với cạnh AC
Theo định lí về góc đối diện với cạnh lớn hơn thì lớn hơn ta có :
\( \Rightarrow \widehat A > \widehat B > \widehat C\)
b)
Vì \(\widehat{A}=\widehat{C}\) nên tam giác ABC cân tại B
\( \Rightarrow BA = BC\)
Áp dụng định lí tổng 3 góc trong tam giác ABC, có:
\( \Rightarrow \widehat B = {180^o} - {100^0} = {80^o}\)
\( \Rightarrow \widehat B > \widehat A=\widehat C\)
\( \Rightarrow AC\) là cạnh lớn nhất tam giác ABC (Quan hệ giữa góc và cạnh đối diện trong tam giác)
Đúng 2
Bình luận (0)
so sánh các cạnh của tam giác ABC,biết rằng:
\(\widehat{A}=90^o\) \(\widehat{B}=45^o\) \(\widehat{C}=45^o\)
Ta có:
\(\widehat{A}>\widehat{B}=\widehat{C}\left(90^0>45^0=45^0\right)\)
`@` Theo định lý quan hệ giữa góc và cạnh đối diện
`->`\(\text{BC > AC = AB}\).
Đúng 0
Bình luận (0)
Cho tam giác ABC,biết \(\widehat{A}+\widehat{B}=120^o;\widehat{A}-\widehat{B}=30^o\)
a) So sánh các cạnh của tam giác đó ?
b) Tia phân giác của \(\widehat{A}\)cắt BC tại,hãy so sánh độ dài DB và CD ?
Cho hai tam giác ABC và A’B’C’ thỏa mãn: BC = B’C’ = 3 cm, \(\widehat B = \widehat {B'} = 60^\circ ,\widehat C = 50^\circ ,\widehat {A'} = 70^\circ \). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
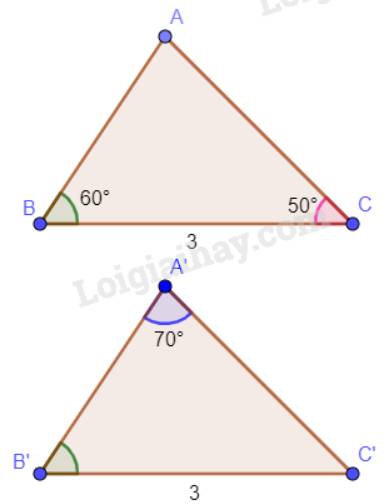
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
Đúng 0
Bình luận (0)
1Tam giác ABC có widehat{A}là góc tù widehat{B}widehat{C}. So sánh độ dài các canhj của tam giác2 Tam giác ABC, AB5cm; BC6cm; AC7cm. Gọi widehat{A1};widehat{B1};widehat{C1}theo thứ tự là góc ngoài tại đỉnh A;B;C của tam giác đó. So sánh widehat{A1;}widehat{B1};widehat{C1} CÁC CẬU ƠI GIÚP TỚ VS NHA. NHANH LÊN HUHUHU
Đọc tiếp
1Tam giác ABC có \(\widehat{A}\)là góc tù \(\widehat{B}>\widehat{C}\). So sánh độ dài các canhj của tam giác
2 Tam giác ABC, AB=5cm; BC=6cm; AC=7cm. Gọi \(\widehat{A1};\widehat{B1};\widehat{C1}\)theo thứ tự là góc ngoài tại đỉnh A;B;C của tam giác đó. So sánh \(\widehat{A1;}\widehat{B1};\widehat{C1}\)
CÁC CẬU ƠI GIÚP TỚ VS NHA. NHANH LÊN HUHUHU