Mn làm và vẽ hình giúp mik với ạ😢

Những câu hỏi liên quan
Giúp mik nhé, mik cần gấp ạ, hộ mik cái hình lun nhé, hihi😊😊😊Cho hình thângBCD có đáy lớn CD và đáy bé AB, chiều cao AH10 cm, S ABCD là 375cm2. Cạnh bên DA và CB cắt nhau tại E. Biết diện tích tam giác ECD gấp 1,5 lần diện tích tam giác EAC. Tính độ dài cạnh đáy CDGIÚP MIK IK MÀ, MIK CẦN GẤP LẮM Ạ, LÀM ƠN, BẠN NÀO TỐT VẼ HỘ MIK CÁI HÌNH NHÉ😩😩😢😢😥😥😭😭🥺🥺🥺
Đọc tiếp
Giúp mik nhé, mik cần gấp ạ, hộ mik cái hình lun nhé, hihi😊😊😊
Cho hình thângBCD có đáy lớn CD và đáy bé AB, chiều cao AH=10 cm, S ABCD là 375cm2. Cạnh bên DA và CB cắt nhau tại E. Biết diện tích tam giác ECD gấp 1,5 lần diện tích tam giác EAC. Tính độ dài cạnh đáy CD
GIÚP MIK IK MÀ, MIK CẦN GẤP LẮM Ạ, LÀM ƠN, BẠN NÀO TỐT VẼ HỘ MIK CÁI HÌNH NHÉ😩😩😢😢😥😥😭😭🥺🥺🥺
Ai xong trước và đúng thì mik nhé😇😇😇😇😇🥺🥺😭😫😫
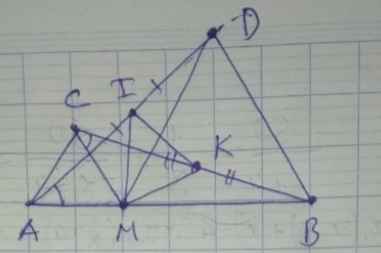
Cho điểm M nằm trên đoạn thẳng AB. Vẽ về một phía của AB các tam giác đều AMC và BMD .
a) Chứng minh rằng AD=CB
b) Gọi I , K theo thứ tự là trung điểm của AD và CB. Tam giác MIK là tam giác gì ?
vẽ hình nha và giải nhanh giúp mình làm ơn!!!😢😢😢😢😢
a) Ta có: \(\widehat{AMD}=\widehat{AMC}+\widehat{CMD}\)
\(=60^0+\widehat{CMD}\) \(\left(1\right)\)
Lại có: \(\widehat{CMB}=\widehat{BMD}+\widehat{CAD}\)
\(=60^0+\widehat{CMD}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\): ⇒ \(\widehat{AMD}=\widehat{CMB}\)
Xét △ AMD và △ CMB có:
CH = AM ( △ AMC đều )
\(\widehat{AMD}=\widehat{CMB}\) ( cmt )
MB = MD ( △ BMD đều )
⇒ △ AMD = △ CMB ( c - g - c )
Do đó: AD = CB ( 2 cạnh tương ứng )
b) Ta có: \(CK=\dfrac{BC}{2}\) ( K là trung điểm CB )
Ta có: \(AI=\dfrac{AD}{2}\) ( I là trung điểm AD )
Mà BC = AD ( cmt ) ⇒ CK = AI
Xét △ AMI và △ CMK có:
CM = AM ( △ AMC đều )
\(\widehat{IAM}=\widehat{KCM}\) ( vì △ AMD = △ CMB )
AI = CK ( cmt )
⇒ △ AMI = △ CMK ( c - g - c )
⇒ MK = MI
⇒ △ IMK cân tại M
Đúng 2
Bình luận (0)
Mn giúp e bài này với ạ:(( thầy giáo cho btvn mà e ko biết làm ntn😢 nhờ mn giúp e với ạ. E cảm ơn🥰🥰
Mọi người ơi giúp mik với ạ , mik đg cần gấppp mai mik học rồi mà mik đg chx làm đc . Cho mik hình vẽ và lời giải thật chi tiết với ạ xong mik sẽ tick ạ mik cảm ơn .
Bài này trong sách là trên mạng có ấy c lên ytb shears cho nhanh
Đúng 0
Bình luận (1)
Mọi người ơi giúp mik với ạ , mik đg cần gấppp mai mik học rồi mà mik đg chx làm đc . Cho mik hình vẽ và lời giải thật chi tiết với ạ xong mik sẽ tick ạ mik cảm ơn .
Giúp mình bài 4 và vẽ hình luôn mn ơi. Tối mình phải nộp rồi😢
a/ Ta có:
- ABCD là hình bình hành => \(AD=BC;AD\text{ // }BC\)
- Xét △ADH và △BKC có:
+ \(AD=BC\left(cmt\right)\)
+ \(\hat{ADH}=\hat{CBK}\left(slt\right)\)
=> \(\text{△ADH = △CBK}\left(c.h-g.n\right)\)
Vậy: \(...
Đúng 0
Bình luận (0)
(Làm lại tại bị lỗi)
a/ - ABCD là hình bình hành => \(AD\text{//}BC;AD=BC\)
- Xét △ADH và △CBK có:
+ \(AD=BC\left(cmt\right)\)
+ \(\hat{ADH}=\hat{CBK}\left(slt\right)\)
=> \(\text{△ADH = △CBK }\left(c.h-g.n\right)\).
Vậy: \(DH=BK\left(đpcm\right)\)
==========
b/ \(AH\text{⊥}HK;CK\text{⊥}HK\)
=> \(AH\text{//}CK\)
Xét tứ giác AHCK có:
- \(AH=CK\left(\text{△ADH = △CBK }\right)\)
- \(AH\text{//}CK\)
Vậy: Tứ giác AHCK là hình bình hành (đpcm)
===========
c/ Hình bình hành AHCK có
- HK là đường chéo
- O là trung điểm của HK
=> O cũng là trung điểm của đường chéo AC (Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Vậy: A, O, H thẳng hàng (đpcm)
Đúng 0
Bình luận (0)
khi thực hiện quyền khiếu nại tố cáo cần đảm bảo yếu tố gì?
mik cần gấp mong mn giúp mik với😢😢😢
Xem chi tiết
1. Bảo đảm về nhận thức
2. Bảo đảm về pháp lý
3. Bảo đảm về sự phối hợp giữa các cơ quan, tổ chức, cá nhân có liên quan
4. 4. Bảo đảm có sự thanh tra, kiểm tra, giám sát việc thi hành
Đúng 3
Bình luận (0)
giúp mình trả lời với vẽ hình đc k ạ, hicc mình cảm ơn nhiều😢
a: Xét ΔBAK và ΔBDK có
BA=BD
\(\widehat{ABK}=\widehat{DBK}\)
BK chung
Do đó: ΔBAK=ΔBDK
b: Ta có: ΔBAK=ΔBDK
nên KA=KD
mà BA=BD
nên BK là đường trung trực của AD
Đúng 2
Bình luận (0)
a)Xét \(\Delta BAK\) và \(\Delta BDK\) có:
AB=BD
\(\widehat{ABK}=\widehat{DBK}\)
BK chung
=> \(\Delta BAK\) = \(\Delta BDK\) (c-g-c)
b)Gọi O là giao điểm của AD và BK
Xét \(\Delta ABO\) và \(\Delta DBO\) có :
BO chung
\(\widehat{ABO}=\widehat{DBO}\)
AB=DB
=> \(\Delta ABO\) và \(\Delta DBO\) (c-g-c)
=> AO=BO (1) ; \(\widehat{AOB}=\widehat{DOB}\)
Có : \(\widehat{AOB}+\widehat{DOB}=180^o\) mà \(\widehat{AOB}=\widehat{DOB}\)
=> \(\widehat{AOB}=\widehat{DOB}=\dfrac{180^o}{2}=90^o\) (2)
Từ (1)(2) => BK là đường trung trực cùa AD
Đúng 1
Bình luận (0)
Giúp e bài n với mn ơi e c.ơn ạ mong mn giúp e😢
\(a,B=4\sqrt{x+1}-3\sqrt{x+1}+\sqrt{x+1}+2\sqrt{x+1}=4\sqrt{x+1}\\ b,B=8\Leftrightarrow4\sqrt{x+1}=8\\ \Leftrightarrow\sqrt{x+1}=2\\ \Leftrightarrow x+1=4\\ \Leftrightarrow x=3\left(tm\right)\)
Đúng 0
Bình luận (0)
Mn giúp mình giải với ạ 😢