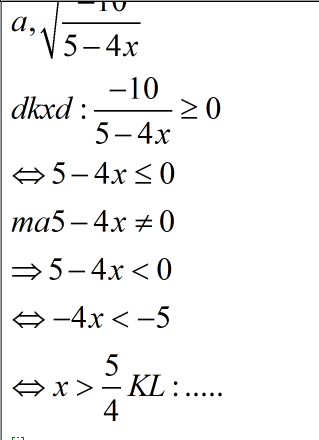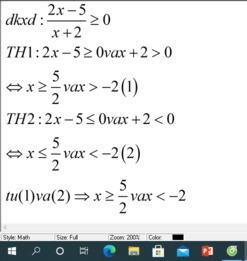Tìm điều kiện xác định của \(\sqrt{\frac{x-2}{x^2-2x+1}}\)

Những câu hỏi liên quan
tìm điều kiện xác định của bất phương trình \(\sqrt{2-x}+x< 2+\sqrt{1-2x}\)
ĐK: \(\left\{{}\begin{matrix}2-x\ge0\\1-2x\ge0\end{matrix}\right.\Leftrightarrow\dfrac{1}{2}\le x\le2\)
Đúng 0
Bình luận (0)
M= \(\left(\frac{2x\sqrt{x}+x-\sqrt{x}}{x\sqrt{x}-1}-\frac{x+\sqrt{x}}{x-1}\right).\frac{x-1}{2x+\sqrt{x}-1}+\frac{\sqrt{x}}{2\sqrt{x}-1}\)
a) Tìm điều kiện xác định của M và rút gọn M
b) Tìm giá trị nhỏ nhất của M
\(A=\frac{x+\sqrt{x^2-2x}}{x-\sqrt{x^2-2x}}-\frac{x-\sqrt{x^2-2x}}{x+\sqrt{x^2-2x}}\)
a) Tìm điều kiện xác định của biểu thức A
b) Rút gọn biểu thức A
c) Tìm giá trị của x để A < 2
a) A xác định \(\Leftrightarrow\hept{\begin{cases}x^2-2x\ge0\\x-\sqrt{x^2-2x}\ne0\\x+\sqrt{x^2-2x}\ne0\end{cases}\Leftrightarrow}\hept{\begin{cases}x< 0\\x\ge2\end{cases}}\)
b) \(A=\frac{x+\sqrt{x^2-2x}}{x-\sqrt{x^2-2x}}-\frac{x-\sqrt{x^2-2x}}{x+\sqrt{x^2-2x}}=\frac{\left(x^2+x^2-2x+2x\sqrt{x^2-2x}\right)-\left(x^2+x^2-2x-2x\sqrt{x^2-2x}\right)}{x^2-\left(x^2-2x\right)}\)\(=\frac{4x\sqrt{x^2-2x}}{2x}=2\sqrt{x^2-2x}\)
c) \(A< 2\Leftrightarrow2\sqrt{x^2-2x}< 2\Leftrightarrow x^2-2x< 1\Leftrightarrow x^2-2x-1< 0\Leftrightarrow1-\sqrt{2}\le x\le1+\sqrt{2}\)
Kết hợp với điều kiện A xác định được : \(2\le x\le1+\sqrt{2}\)
Vậy \(A< 2\Leftrightarrow2\le x\le1+\sqrt{2}\)
Đúng 0
Bình luận (0)
Cho biểu thức: A=\(\frac{x+\sqrt{x^2-2x}}{x-\sqrt{x^2}-2x}-\frac{x-\sqrt{x^2-2x}}{x+\sqrt{x^2}-2x}\\ \)
a)Tìm điều kiện xác định của biểu thức A
b) Rút gọn biểu thức A
c)Tìm một giá trị của x để A<2
Tìm điều kiện xác định
\(\sqrt{x^2-2x+1}+\sqrt{x^2-6x+9}=1\)
\(\sqrt{x^2-2x+1}+\sqrt{x^2-4x+4}=3\)
a: ĐKXĐ: \(x\in R\)
b: ĐKXĐ: \(x\in R\)
Đúng 0
Bình luận (0)
Tìm điều kiện xác định của biểu thức sau:
a)\(\frac{1}{1-\sqrt{x^2}-3}\)
b)\(\frac{\sqrt{16-x^2}}{\sqrt{2x+1}}+\sqrt{x^2-8x+14}\)
Mình nghĩ đề câu a) là \(\frac{1}{1-\sqrt{x^2-3}}\) khi đó
\(1-\sqrt{x^2-3}\ne0\Rightarrow\sqrt{x^2-3}\ne1\Rightarrow x\ne\pm2\)và \(x^2-3\ge0\Leftrightarrow-\sqrt{3}\le x\le\sqrt{3}\)
b)
\(\sqrt{16-x^2}\ge0;\sqrt{2x+1}\ge0;\sqrt{x^2-8x+14}\ge0\)và \(\sqrt{2x+1}\ne0\)
\(\Leftrightarrow-4\le x\le4;x\ge-\frac{1}{2};4-\sqrt{2}\le x\le4+\sqrt{2};x\ne\frac{1}{2}\)
Như vậy \(-\frac{1}{2}< x\le4+\sqrt{2}\)
Tìm điều kiện xác định của biểu thức : B = \(\sqrt{x^2-3x}\) + \(\sqrt{\dfrac{x-5}{x-1}}\)- \(\sqrt[3]{2x-1}\)
Tìm điều kiện xác định của các biểu thức sau:
$\sqrt{x^{2} - 4x + 3}$
$\sqrt{x^{2} - 7x + 12}$
$\sqrt{x^{2} - 9x + 20}$
$\sqrt{-x^{2} + 2x - 1}$
a: ĐKXĐ: (x-1)(x-3)>=0
=>x>=3 hoặc x<=1
b: ĐKXĐ: (x-4)(x-3)>=0
=>x>=4 hoặc x<=3
c: ĐKXĐ: (x-5)(x-4)>=0
=>x>=5 hoặc x<=4
Đúng 0
Bình luận (0)
Tìm điều kiện xác định của các biểu thức: a) \(\sqrt{\dfrac{-10}{5-4x}}\) b)\(\sqrt{\dfrac{2x-5}{x+2}}\) c)\(\sqrt{2-x^2}\) d)\(\sqrt{1-\sqrt{x-1}}\) |