Hình ở ảnh chụp
b) BC²=3AH²+BE²+CF²
Helpp me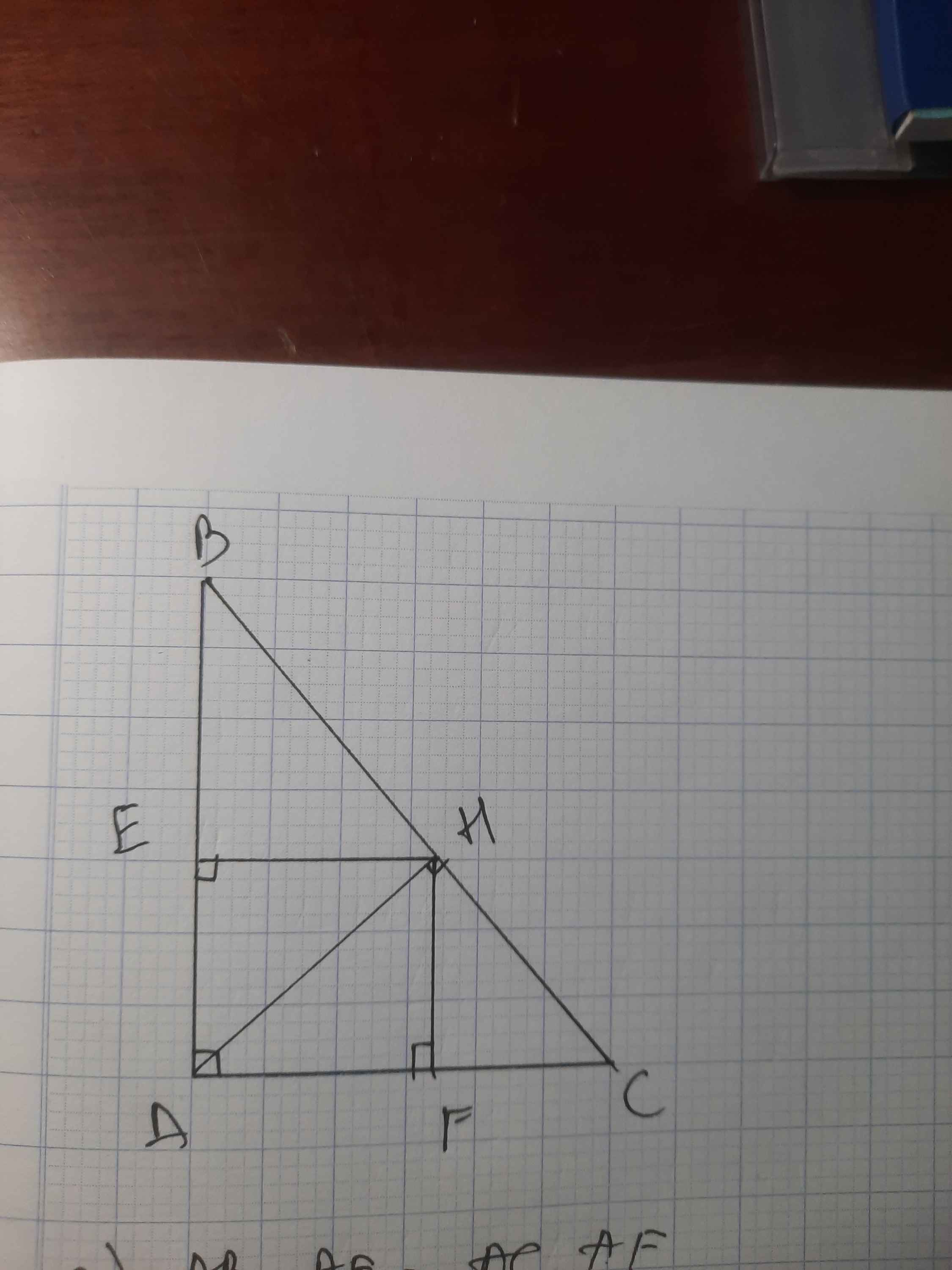

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB, AC. Chứng minh:
a) \(BC^2=3AH^2+BE^2+CF^2\)
b) \(\dfrac{AB^3}{AC^3}=\dfrac{BE}{CF}\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(BE\cdot BA=BH^2\)
hay \(BE=\dfrac{BH^2}{BA}\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền CA, ta được:
\(CF\cdot CA=CH^2\)
hay \(CF=\dfrac{CH^2}{CA}\)
Ta có: \(\dfrac{BE}{CF}=\dfrac{BH^2}{AB}:\dfrac{CH^2}{CA}\)
\(=\dfrac{BH^2}{CH^2}\cdot\dfrac{AC}{AB}\)
\(=\dfrac{AB^4\cdot AC}{AC^4\cdot AC}=\dfrac{AB^3}{AC^3}\)
Đúng 0
Bình luận (1)
CM:
1) BC^2 = BE^2 + CF^2 + 3AH^2
2) AH^3 = BC.BE.CF = BC.HE.HF
3) BE^2 = BH^3/BC
4) CF^2 = CH^3/BC
Cho ΔABC vuông tại A; đường cao AH. Gọi E, F lần lượt là hình chiếu của H lên AB, AC.
a) C/m: AE.AB = AF.AC
b) C/m: \(BC^2=3AH^2+BE^2+CF^2\)
c) C/m: \(\frac{AB^3}{AC^3}=\frac{BE}{CF}\)
Cho tam giac ABC vuông tại A có đường cao AH. Gọi E, F lần lượt là các hình chiếu của H trên AB, AC.
a/ CM \(AH^2=AE.AB\)
b/ CM \(BC^2=3AH^2+BE^2+CF^2\)
c/ CM \(\frac{AB^3}{AC^3}=\frac{BE}{CF}\)
Cho \(\Delta ABC\)vuông tại A, đường cao AH . Gọi E và F là hình chiếu của H trên AB và AC. CMR:
a. \(AH^3=BC.BE.CF\)
b.\(HB.HC=AE.EB+FA.FC\)
c.\(BC^2=3AH^2+BE^2+CF^2\)
d.\(\sqrt[3]{BE^2}+\sqrt[3]{CF^2}=\sqrt[3]{BC^2}\)
Cho tam giác ABC vuông tại A, AH là đường cao; HE , HF lần lượt là các đường cao của tam giác AHB , AHC . CMR:
a) \(BC^2=3AH+BE^2+CF^2\)
b) \(\sqrt[3]{BE^2}+\sqrt[3]{CF^2}=\sqrt[3]{BC^2}\)
giải giùm!
1. Cho tam giác ABC vuông tại A có AH vuông góc với BC . Cạnh HE , HF là đường cao của tam giác AHB và tam giác AHCa) Chứng minh BC2 3AH2 + BE2 + CF2b) Cho BC 2a cố định . Tìm GTNN của BE2 + CF2c) Chứng minh BE2 frac{BH^3}{BC}2. Cho tam giác ABC , có AH vuông góc với BC . Gọi E , F lần lượt là hình chiếu của H trên AB , AC . Biết AH x , BC 2aa) Chứng minh AH3 BC . BE . CF BC . HE . HFb) Tính diện tích tam giác AEF theo a và x . Tìm x để diện tích tam giác AEF đạt GTLN
Đọc tiếp
1. Cho tam giác ABC vuông tại A có AH vuông góc với BC . Cạnh HE , HF là đường cao của tam giác AHB và tam giác AHC
a) Chứng minh BC2 = 3AH2 + BE2 + CF2
b) Cho BC = 2a cố định . Tìm GTNN của BE2 + CF2
c) Chứng minh BE2 =\(\frac{BH^3}{BC}\)
2. Cho tam giác ABC , có AH vuông góc với BC . Gọi E , F lần lượt là hình chiếu của H trên AB , AC . Biết AH = x , BC = 2a
a) Chứng minh AH3 = BC . BE . CF = BC . HE . HF
b) Tính diện tích tam giác AEF theo a và x . Tìm x để diện tích tam giác AEF đạt GTLN
a, bc^2 = ab^2 +ac^2
<=.> (ae+eb)^2 +(af+fc)^2
<=.>AE^2 +2 AE.EB +EB^2 +AF^2+FC^2+2AF,FC
<=> EF^2 +EB^2 +CF^2 +2.(EH^2+FH^2)
<=>EB^2 +CF^2 + AH ^2 + 2 AH^2 vì tứ giác EHAF là hcn suy ra AH =EF
<=>EB^2 +CF^2+3 AH^2 (đpcm)
b, cb =2a là thế nào vậy
Đúng 2
Bình luận (0)
câu a sai vì EHFA không phải hcn , phần trên cũng sai
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho BC có dạng 2a (a 0) và điểm A di động sao cho widehat{BAC}90^o. Kẻ AHperp BCtại H. Gọi HE, HF lần lượt là đường cao của Delta ABHtext{ và }Delta ACHtext{a) CMR}:3AH^2+BE^2+CF^2BC^2text{b) Tìm điều kiện của }Delta ABCtext{ để }BE^2+CF^2text{ đạt GTNN}Các bạn chỉ cần làm giúp mk bài a) thôi, làm được bài b) thì càng tốtPLEASE HELP ME
Đọc tiếp
Cho BC có dạng 2a (a > 0) và điểm A di động sao cho \(\widehat{BAC}=90^o\). Kẻ \(AH\perp BC\)tại H. Gọi HE, HF lần lượt là đường cao của \(\Delta ABH\text{ và }\Delta ACH\)
\(\text{a) CMR}:3AH^2+BE^2+CF^2=BC^2\)
\(\text{b) Tìm điều kiện của }\Delta ABC\text{ để }BE^2+CF^2\text{ đạt GTNN}\)
Các bạn chỉ cần làm giúp mk bài a) thôi, làm được bài b) thì càng tốt
PLEASE HELP ME
a,BC^2 = AB^2 + AC^2.
AB^2= AH^2 + HB^2= AH^2 + HE^2 + BE^2
AC^2= AH^2 + CH^2 = AH^2 + CF^2 + FH^2
Cộng AB^2 và AC^2 rồi ghép HE^2 + FH^2 = AH^2.
Đúng 0
Bình luận (0)
ta de co tu giac AEHF la hinh chu nhat
=>AH=EF
ma EF^2=HE^2+HF^2(chu vi tam giac HEFvuông)
=>AH^2=HE^2+HF^2
ap dung dinh ly pytago cho cac tam giac ABC AHC AHB ta co
AB^2=AH^2+BH^2
AC^2=AH^2+HC^2
=>AB^2+AB^2=BH^2+CH^2+2AH^2
ma BH^2=BE^2+HE^2 ; CF^2+HF^2=CH^2;AB^2+AC^2=BC^2
=>BC^2=BE^2+CF^2+2AH^2+HE^2+HF^2=3AH^2+CF^2+BE^2
Đúng 0
Bình luận (0)
https://h.vn/hoi-dap/question/405985.html
câu b bạn xem ở đây nhé
Chúc học tốt!!!!!!!!!!!!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, AH là đường ca; HE, HF lần lượt là đường cao của tam giác AHB, tam giác AHC. CMR:
a. BC2 = 3AH2 + BE2 + CF2
b.\(\sqrt[3]{BE^2}\)+ \(\sqrt[3]{CF^2}\)= \(\sqrt[3]{BC^2}\)
a) ta có: \(BC^2=\left(BH+CH\right)^2=BH^2+CH^2+2BH.CH\)
=\(BE^2+EH^2+FH^2+CF^2+2AH^2\)
\(=BE^2+CF^2+3AH^2\)(đpcm)
b) đơn giản đi, ta cần chứng minh \(\sqrt[3]{\frac{BE^2}{BC^2}}+\sqrt[3]{\frac{CF^2}{BC^2}}=1\)
Ta có: \(BE=\frac{BH^2}{AB};BC=\frac{AB^2}{BH}\Rightarrow\frac{BE}{BC}=\frac{BH^3}{AB^3}\)
Thiết lập tương tự \(\Rightarrow VT=\frac{BH^2}{AB^2}+\frac{CH^2}{AC^2}\)
Việc còn lại cm nó =1,xin nhường chủ tus
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH . Gọi E F lần lượt là đường chiếu của h trên AB AC Chứng minh rằng:
a. BC² =3AH²+BE²+CF²
b. \(\dfrac{ }{ }\) AB³/AC³= BE/CF
c. AH³= BC.BE.CF
= BC.HE.HF
b: \(\dfrac{BE}{CF}=\dfrac{HB^2}{AB}:\dfrac{HC^2}{AC}=\dfrac{HB^2}{HC^2}\cdot\dfrac{AC}{AB}=\dfrac{AB^4}{AC^4}\cdot\dfrac{AC}{AB}=\dfrac{AB^3}{AC^3}\)
c: \(BC\cdot BE\cdot CF\)
\(=BC\cdot\dfrac{BH^2}{AB}\cdot\dfrac{CH^2}{AC}\)
\(=AH^4\cdot\dfrac{BC}{AB\cdot AC}\)
\(=AH^4\cdot\dfrac{BC}{AH\cdot BC}=AH^3\)
Đúng 0
Bình luận (0)















