B1:
biết: u1=a; u2=-b; un+2=un+1-un với n thuộc N*. Tính u2020
B2:
Cho x, y thoa mãn: x2+(x-y)2=0
tính A=2021x2020y2019-2019x2019y2018+2018x2017y2016-100
Ai đó làm ơn giúp mình với ạ, mình cảm ơn rất nhiều 1.Cho cấp số nhân(Un). Tìm U1 và q. Biết rằng a. U1 + u6= 165; u3 + u4=60 2. Tìm số hạng đầu và công bội của cấp số nhân, biết a. U4- u2= 72; U5- u3=144 b. u1- u3+u5=65;u1+u7=325 c. u3+u5=90; u2-u6=240 d. u1+u2+u3=14; u1.u2.u3=64
Để tìm U1 và q, ta sử dụng hệ phương trình sau:
U1 + U6 = 165U3 + U4 = 60Đầu tiên, ta sử dụng phương trình thứ hai để tìm U3: U3 = 60 - U4
Sau đó, thay giá trị của U3 vào phương trình thứ nhất: U1 + U6 = 165 U1 + (U3 + 3q) = 165 U1 + (60 - U4 + 3q) = 165 U1 - U4 + 3q = 105 (1)
Tiếp theo, ta sử dụng phương trình thứ nhất để tìm U6: U6 = 165 - U1
Thay giá trị của U6 vào phương trình thứ hai: U3 + U4 = 60 (60 - U4) + U4 = 60 60 = 60 (2)
Từ phương trình (2), ta thấy rằng phương trình không chứa U4, do đó không thể giải ra giá trị của U4. Vì vậy, không thể tìm được giá trị cụ thể của U1 và q chỉ từ hai phương trình đã cho.
Để tìm số hạng đầu và công bội của cấp số nhân, ta sử dụng các phương trình đã cho:
a. U4 - U2 = 72 U5 - U3 = 144
Đầu tiên, ta sử dụng phương trình thứ nhất để tìm U4: U4 = U2 + 72
Sau đó, thay giá trị của U4 vào phương trình thứ hai: U5 - U3 = 144 (U2 + 2q) - U3 = 144 U2 - U3 + 2q = 144 (3)
Từ phương trình (3), ta thấy rằng phương trình không chứa U2, do đó không thể giải ra giá trị của U2 và q chỉ từ hai phương trình đã cho.
b. U1 - U3 + U5 = 65 U1 + U7 = 325
Đầu tiên, ta sử dụng phương trình thứ hai để tìm U7: U7 = 325 - U1
Sau đó, thay giá trị của U7 vào phương trình thứ nhất: U1 - U3 + U5 = 65 U1 - U3 + (U1 + 6q) = 65 2U1 - U3 + 6q = 65 (4)
Từ phương trình (4), ta thấy rằng phương trình không chứa U3, do đó không thể giải ra giá trị của U1 và q chỉ từ hai phương trình đã cho.
c. U3 + U5 = 90 U2 - U6 = 240
Đầu tiên, ta sử dụng phương trình thứ hai để tìm U6: U6 = U2 - 240
Sau đó, thay giá trị của U6 vào phương trình thứ nhất: U3 + U5 = 90 U3 + (U2 - 240 + 4q) = 90 U3 + U2 - 240 + 4q = 90 U3 + U2 + 4q = 330 (5)
Từ phương trình (5), ta thấy rằng phương trình không chứa U2, do đó không thể giải ra giá trị của U2 và q chỉ từ hai phương trình đã cho.
d. U1 + U2 + U3 = 14 U1 * U2 * U3 = 64
Đầu tiên, ta sử dụng phương trình thứ nhất để tìm U3: U3 = 14 - U1 - U2
Sau đó, thay giá trị của U3 vào phương trình thứ hai: U1 * U2 * (14 - U1 - U2) = 64
Phương trình này có dạng bậc ba và không thể giải ra giá trị cụ thể của U1 và U2 chỉ từ hai phương trình đã cho.
Tóm lại, không thể tìm được giá trị cụ thể của số hạng đầu và công bội của cấp số nhân chỉ từ các phương trình đã cho.
Cho hình vẽ sau
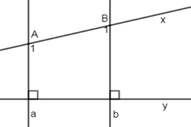
Biết a ⊥ y , b ⊥ y , A 1 ^ - B 1 ^ = 40 o . Tính B 1 ^
A. 110 °
B. 70 °
C. 80 °
D. 90 °
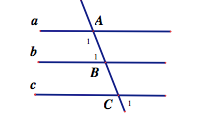
Cho hình vẽ. Biết A1 + B1 = 180độ , B1 = C1. Chứng minh rằng A//B//C ?
\(\hat{A}_1+\hat{B}_1=180^o\Rightarrow a\text{ // }b\left(tcp\right)\)
\(\hat{B}_1=\hat{C}_1\Rightarrow b\text{ // }c\left(đv\right)\)
\(\Rightarrow a\text{ // }b\text{ // }c\left(đpcm\right)\)
Ai gioi toan CASIO ko ak? Giup mik vs
3.2.Cho dãy số u1;u2;u3;...;un;Biết u1= 25 ; u2=u1+121;u3=u1+u2+441;u4=u1+u2+u3+1225;
u5= u1+u2+u3+u4+2809;...
a)Viết quy trình bấm phím liên tục tính un
b)Tính U25;u50
 Toshiro Kiyoshi34GP
Toshiro Kiyoshi34GP
 Nguyễn Huy Tú30GP
Nguyễn Huy Tú30GP
 Hồng Phúc Nguyễn24GP
Hồng Phúc Nguyễn24GP
 Akai Haruma21GP
Akai Haruma21GP
 nguyen van tuan19GP
nguyen van tuan19GP
 T.Thùy Ninh19GP
T.Thùy Ninh19GP
 Xuân Tuấn Trịnh11GP
Xuân Tuấn Trịnh11GP
 Nguyen Ngoc Anh Linh10GP
Nguyen Ngoc Anh Linh10GP
 Nguyen Bao Linh9GP
Nguyen Bao Linh9GP
Biết a vg c, b vg c, B1-A1=20 độ. Tính số đo góc A1 và B1.
a⊥b, a⊥c⇒b//c
ta có: A1 và B1 là 2 góc trong cùng phái nên A1+B1=180o
Ta có: A1+B1=180o, B1-A1=20o⇒A1+B1-B1+A1=180o-20o
⇒ 2A1=160o
⇒A1=80o
A1+B1=180o ⇒80o+B1=180o⇒B1=100o
Vậy A1=80o, B1=100o
a) Biết A3= B1. CMR: A2 + B1= 180 độ
b) Bt A1 = B1. CM: A3 = B1; A2 = B4
c) Bt A2= B4 và A1= 72 độ. Tính các góc còn lại
a) Biết A3= B1. CMR: A2 + B1= 180 độ
b) Bt A1 = B1. CM: A3 = B1; A2 = B4
c) Bt A2= B4 và A1= 72 độ. Tính các góc còn lại
Trên hình biết a // b và góc B2=40 độ:
a) Tính góc A1
b) So sánh góc A3 và B1
c) Tính góc A2+B1
\(a,a//b\Rightarrow\widehat{B_2}+\widehat{A_1}=180^0\left(trong.cùng.phía\right)\\ \Rightarrow\widehat{A_1}=180^0-40^0=140^0\\ b,a//b\Rightarrow\widehat{A_1}=\widehat{B_1}\left(đồng.vị\right)\\ Mà.\widehat{A_1}=\widehat{A_3}\left(đối.đỉnh\right)\\ \Rightarrow\widehat{A_3}=\widehat{B_1}\\ c,Ta.có.\widehat{A_2}+\widehat{B_1}=\widehat{A_2}+\widehat{A_1}=180^0\left(kề.bù\right)\)
a. Ta có: a // b
=> \(\widehat{B_2}+\widehat{A_1}=180^o\) (2 góc trong cùng phía)
Mà \(\widehat{B_2}=40^o\)
=> \(\widehat{A_1}=180^o-40^o=140^o\)
b. Ta có: \(\widehat{A_1}=\widehat{B_3}\) (so le trong) (1)
Ta lại có: \(\left\{{}\begin{matrix}\widehat{A_1}=\widehat{A_3}\left(ĐĐ\right)\\\widehat{B_1}=\widehat{B_3}\left(ĐĐ\right)\end{matrix}\right.\) (2)
Từ (1) và (2), suy ra:
\(\widehat{A_3}=\widehat{B_1}\)
c. Ta có: a // b
=> \(\widehat{A_1}=\widehat{B_1}=140^o\) (đồng vị)
\(\widehat{B_2}=\widehat{A_2}=40^o\) (đồng vị)
=> \(\widehat{A_2}+\widehat{B_1}=140^o+40^o=180^o\)
Giả sử trong các ô A1, B1 lần lượt chứa các số -4, 3. Em hãy cho biết kết quả của các công thức tính sau:
a) = SUM(A1, B1)
b) = SUM(A1,B1,B1)
c) = SUM(A1, B1, -5)
d) = SUM(A1, B1, 2)
e) =AVERAGE(A1, B1, 4)
g) =AVERAGE(A1, B1, 5,0)
a) = SUM(A1, B1) Kết quả thực hiện là : - 1
b) = SUM(A1,B1,B1) Kết quả thực hiện là : 2
c) = SUM(A1, B1, -5) Kết quả thực hiện là : - 6
d) = SUM(A1, B1, 2) Kết quả thực hiện là : 1
e) = AVERAGE(A1, B1, 4) Kết quả thực hiện là : 1
g) = AVERAGE(A1, B1, 5, 0) Kết quả thực hiện là : 1
Giả sử trong các ô A1, B1 lần lượt chứa các số -4,3. Em hãy cho biết kết quả các công thức tính sau:
a) =SUM(A1, B1); b) =SUM(A1,B1,B1); c) =SUM(A1,B1,-5);b) =SUM(A1, B1, 2); e) =AVERAGE(A1,B1,4); f) =AVERAGE(A1,B1,5,0);
Theo giả thiết: A1 = -4; B1 = 3, ta có:
a) = A1+ B1 = -1;
b) = A1+ B1+ B1 =2;
c) = A1+ B1+ (-5) = -6;
d) = A1+ B1+ 2 = 1;
e) = (A1+ B1+ 4)/3 = 1;
f) = (A1+B1+ 5+0)/4 = 1;
Thế thui nha :)?