Giá trị a2+b2 biết
\(\frac{a}{b}\)=\(\frac{2.1}{2.8}\)và 5a - 4b =-1
Cho ba số thực dương a,b,c thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 b - 6 c = 10 và a + c=2 . Tính giá trị biểu thức P = 3a + 2b + c khi Q = a 2 + b 2 + c 2 - 14 a - 8 b + 18 c đạt giá trị lớn nhất.
A. 10
B. -10
C. 12
D. -12
Đáp án D

Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu (S) và mặt phẳng (P) sao cho KM lớn nhất





\(\frac{a}{b}=\frac{2,1}{2,7}\),5a-4b=-1.giá trị của (a-b)2
Ta có: \(\frac{a}{b}=\frac{2,1}{2,7}\) => \(\frac{a}{2,1}=\frac{b}{2,7}\) => \(\frac{5a}{10,5}=\frac{4b}{10,8}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{5a}{10,5}=\frac{4b}{10,8}=\frac{5a-4b}{10,5-10,8}=\frac{-1}{-0,3}=\frac{1}{0,3}\)
=> 5a=\(\frac{1}{0,3}.10,5=35\) => a=7
4b=\(\frac{1}{0,3}.10,8=36\) => b=9
Vậy a=7; b=9
ta có :\(\frac{a}{b}\) =\(\frac{2,1}{2,7}\) =>\(\frac{a}{2,1}\) =\(\frac{b}{2,7}\)
=>\(\frac{5a}{10,5}\) =\(\frac{4b}{10,8}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\frac{5a}{10,5}\) =\(\frac{4b}{10,8}\) =\(\frac{5a-4b}{10,5-10,8}\) =\(\frac{-1}{-0,3}\)
\(\frac{a}{2,1}\) =\(\frac{1}{0,3}\) => a=7
\(\frac{b}{2,7}\) =\(\frac{1}{0,3}\) =>b=9
=>(a-b)2= (7-9)2=(-2)2=4
Cho a,b là các số thực thỏa mãn a 2 + b 2 > 1 và log a 2 + b 2 a + b ≥ 1 . Giá trị lớn nhất của biểu thức P = 2a + 4b - 3 bằng
A. 1 10
B. 10 2
C. 10
D. 2 10
Ta có ![]()
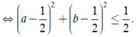
Ta có 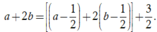
Áp dụng bất đẳng thức Bunhiacopxky, ta có
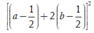
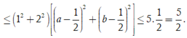
Do đó 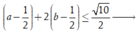
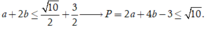
Dấu "x" xảy ra 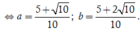
Chọn C.
Ta thấy (1) là hình tròn tâm ![]()
Ta có ![]() Xem đây là phương trình đường thẳng.
Xem đây là phương trình đường thẳng.
Để đường thẳng và hình tròn có điểm chung ![]()

Cho hai số thực a,b thỏa mãn điều kiện a 2 + b 2 > 1 và log a 2 + b 2 a + b ≥ 1 . Giá trị lớn nhất của biểu thức P = 2a + 4b – 3 là
A. 2 10
B. 10
C. 10 2
D. 1 10
cho các số a,b,c thõa mãn 5a=4b=2c và a-b+c=-18. tính giá trị của biểu thức \(P=\left(\frac{2}{a}+\frac{5}{b}+\frac{5}{c}\right)^{2017}\)
Cho biết (a+b) =1 và ab=-12 giá trị của a2 +b2 bằng
\(a^2+b^2=\left(a+b\right)^2-2ab\)
=1+24
=25
1 Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
2 Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
3 Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
2:
a: =>a^2+2ab+b^2-2a^2-2b^2<=0
=>-(a^2-2ab+b^2)<=0
=>(a-b)^2>=0(luôn đúng)
b; =>a^2+b^2+c^2+2ab+2ac+2bc-3a^2-3b^2-3c^2<=0
=>-(2a^2+2b^2+2c^2-2ab-2ac-2bc)<=0
=>(a-b)^2+(b-c)^2+(a-c)^2>=0(luôn đúng)
1,Giá trị x thỏa mãn : \(\frac{x}{-8}=\frac{-18}{x}\)
2, Tập hợp giá trị x nguyên thỏa mãn : | 2x-7| + | 2x + 1 | \(\le\) 8
3,Cho \(\frac{a}{b}=\frac{2,1}{2,7}\) ; 5a- 4b = -1 . Giá trị \(\left(a-b\right)^2\) là
4, Cho \(\frac{a}{b}=\frac{9,6}{12,8};a^2+b^2=25\) . Giá trị | a + b| là ......
Bài 1:
\(\frac{x}{-8}=\frac{-18}{x}\)
\(\Rightarrow x^2=144\)
\(\Rightarrow x=\pm12\)
Vậy \(x=\pm12\)
Bài 3:
Giải:
Ta có: \(\frac{a}{b}=\frac{2,1}{2,7}\Rightarrow\frac{a}{2,1}=\frac{b}{2,7}\Rightarrow\frac{a}{21}=\frac{b}{27}\Rightarrow\frac{a}{7}=\frac{b}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{7}=\frac{b}{9}=\frac{5a}{35}=\frac{4b}{36}=\frac{5a-4b}{35-36}=\frac{-1}{-1}=1\)
+) \(\frac{a}{7}=1\Rightarrow a=7\)
+) \(\frac{b}{9}=1\Rightarrow b=9\)
\(\Rightarrow\left(a-b\right)^2=\left(7-9\right)^2=\left(-2\right)^2=4\)
Vậy \(\left(a-b\right)^2=4\)
Bài 4:
Giải:
Ta có: \(\frac{a}{b}=\frac{9,6}{12,8}\Rightarrow\frac{a}{9,6}=\frac{b}{12,8}\Rightarrow\frac{a}{96}=\frac{b}{128}\Rightarrow\frac{a}{3}=\frac{b}{4}\)
Đặt \(\frac{a}{3}=\frac{b}{4}=k\)
\(\Rightarrow a=3k,b=4k\)
Mà \(a^2+b^2=25\)
\(\Rightarrow\left(3k\right)^2+\left(4k\right)^2=25\)
\(\Rightarrow9.k^2+16.k^2=25\)
\(\Rightarrow25k^2=25\)
\(\Rightarrow k^2=1\)
\(\Rightarrow k=\pm1\)
+) \(k=1\Rightarrow a=3;b=4\)
+) \(k=-1\Rightarrow a=-3;b=-4\)
\(\Rightarrow\left|a+b\right|=\left|3+4\right|=\left|-3+-4\right|=7\)
Vậy \(\left|a+b\right|=7\)
Áp dụng BĐT
\(\left|a\right|+\left|b\right|\ge\left|a+b\right|\)Ta có:
\(\left|2x-7\right|+\left|2x+1\right|=\left|2x-7\right|+\left|-2x-1\right|\ge\left|2x-7+\left(-2x-1\right)\right|=8\)
Mà \(\left|2x-7\right|+\left|2x+1\right|\ge\)8 nên không có số nguyên x nào thỏa mãn đề ra
Biết rằng các số thực a, b thay đổi sao cho hàm số f x = − x 3 + x + a 3 + x + b 3 đồng biến trên khoảng − ∞ ; + ∞ . Tìm giá trị nhỏ nhất của biểu thức P = a 2 + b 2 − 4 a − 4 b + 2.
A. -4
B. -2
C. 0
D. 2
Đáp án B
Ta có
f ' x = 3 x + a 2 + x + b 2 − x 2 = 3 x 2 + 2 a + b x + a 2 + b 2
Để hàm số luôn đồng biến trên − ∞ ; + ∞
thì Δ ' = a + b 2 − a 2 + b 2 ≤ 0 ⇔ a b ≤ 0
Ta có
P = a 2 + b 2 − 4 a − 4 b + 2 = a + b − 2 2 − 2 a b − 2 ≥ − 2.
Dâu bằng xảy ra khi a + b = 2 a b = 0 ⇔ a = 2 b = 0 hoặc ngược lại.