Tìm x,y biết
x2+ y4=0
Những câu hỏi liên quan
Tìm số nguyên x. biết
x2=-25
\(x^2=-25\)
Vì \(x^2\ge0\forall x\)
Mà \(x^2=-25\) (vô lí)
Vậy: \(x\in\varnothing\)
Đúng 3
Bình luận (0)
Xem thêm câu trả lời
tìm x biết
x2+5x=0
phân tích đa thức sau thành nhân tử
x2-2x-xy+2y
HELP 28 phút nữa thi rồi
\(x^2+5x=0\Leftrightarrow x\left(x+5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(x^2-2x-xy+2y=\left(x^2-xy\right)-2\left(x-y\right)=x\left(x-y\right)-2\left(x-y\right)=\left(x-y\right)\left(x-2\right)\)
Đúng 2
Bình luận (0)
tìm x và y
4 phần x = y phần -20 = 12 phần -15
\(\dfrac{4}{x}=\dfrac{y}{-20}=\dfrac{12}{-15}\)
\(\Rightarrow\dfrac{4}{x}=\dfrac{y}{-20}=-\dfrac{4}{5}\)
\(\Rightarrow\left\{{}\begin{matrix}x=4:-\dfrac{4}{5}=-5\\y=-\dfrac{4}{5}.\left(-20\right)=16\end{matrix}\right.\)
Đúng 3
Bình luận (0)
cho x+y+z=0. chứng minh 2(x4+y4+z4)=(x2+y2+z2)2
\(\left(x+y+z\right)^2=x^2+y^2+z^2+2xy+2yz+2xz\) Thay x+y+z=0 vào
\(\Rightarrow0=x^2+y^2+z^2+2\left(xy+yz+xz\right)\)
\(\Leftrightarrow x^2+y^2+z^2=-2\left(xy+yz+xz\right)\) (1)
Ta có
\(\left(x^2+y^2+z^2\right)^2=x^4+y^4+z^4+2x^2y^2+2y^2z^2+2x^2z^2\) (2)
Bình phương 2 vế của (1)
\(\left(x^2+y^2+z^2\right)^2=4\left(xy+yz+xz\right)^2\)
\(\Leftrightarrow\left(x^2+y^2+z^2\right)^2=4\left(x^2y^2+y^2z^2+x^2z^2+2xy^2z+2xyz^2+2x^2yz\right)\)
\(\Leftrightarrow\left(x^2+y^2+z^2\right)^2=4\left[x^2y^2+y^2z^2+x^2z^2+2xyz\left(x+y+z\right)\right]\)
Do x+y+z=0 nên
\(\left(x^2+y^2+z^2\right)^2=4\left(x^2y^2+y^2z^2+x^2z^2\right)\)
\(\Rightarrow\dfrac{\left(x^2+y^2+z^2\right)^2}{2}=2x^2y^2+2y^2z^2+2x^2z^2\) (3)
Thay (3) vào (2)
\(\left(x^2+y^2+z^2\right)^2=x^4+y^4+z^4+\dfrac{\left(x^2+y^2+z^2\right)^2}{2}\)
\(\Rightarrow2\left(x^4+y^4+z^4\right)=\left(x^2+y^2+z^2\right)^2\) (đpcm)
Đúng 1
Bình luận (0)
Tìm ba số x, y, z biết rằng
x
2
y
3
;
y
4
z
5
và x + y - z 20 A. x 32; y 48; z 60 B. x 16; y 24; z 30 C. x 24; y 36; z 45 D. x 8; y 12; z 15
Đọc tiếp
Tìm ba số x, y, z biết rằng x 2 = y 3 ; y 4 = z 5 và x + y - z = 20
A. x = 32; y = 48; z = 60
B. x = 16; y = 24; z = 30
C. x = 24; y = 36; z = 45
D. x = 8; y = 12; z = 15
cho x+y+z=3
tìm minM: x4+y4+z4+12(1-x)(1-y)(1-z)
Tìm ba số x, y, z biết x 2 = y 3 , y 4 = z 5 v à x + y - z = 10 và x + y - z = 10
Theo đề bài ta có :
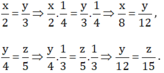
Do đó ta có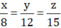 
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
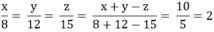
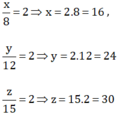
Vậy x =16 ; y = 24 ; z =30
Đúng 0
Bình luận (0)
Tìm các số x y z biết x/2 = y/3;y4 = Z/5 tính x cộng y trừ Z = 25
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{25}{5}=5\)
Do đó: x=40; y=60; z=75
Đúng 0
Bình luận (0)
Cho x,y,z là số thực tùy ý biết x+y+z=0 và -1≤x≤1; -1≤y≤1; -1≤z≤1
Chứng minh x2+y4+z6≤2
tính giá tri của các bieur thưc sau
a=x2(x+y)-y2(x+y)+x2-y2+2(x+y)+3 biết x+y+1=0
b=x4-xy3+x3y-y4+1 biết x+y=0
