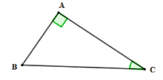
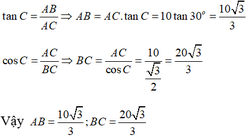Cho ∆ABC vuông tại A có C^ = 30° ; đường cao AH. Trên tia đối của HB lấy D sao cho HD = HB. Chứng minh: a) AD = AB b) ∆ABD là ∆ đều c) vẽ CE vuông góc với đường thẳng AD ( E thuộc AD). Chứng minh: AH = CE

Những câu hỏi liên quan
a ) cho tam giác ABC vuông tại A , góc B = 30 độ
CMR : AC = 1/2 BC
b ) cho tam giác ABC vuông tại A có AB = 1/2 BC
CMR : góc C = 30 độ
Kẻ trung tuyến AM, AM = 1/2 BC = MB = MC
a) Nêu góc B = 30 độ thì góc C bằng 60 độ
Tam giác MAC cân tại M có góc C bằng 60 độ nên nó là tam giác đều => AC = MC = 1/2 BC
b) Nếu AC = 1/2 BC => Tam giác MAC đều vì AC = 1/2 BC = MC = MA
=> Góc C bằng 60 độ
Trong tam giác ABC có góc A = 90 độ, góc C = 60 độ => góc B = 30 độ
Đúng 0
Bình luận (0)
sao lại làm thế này
Cho tam giác ABC vuông tại A có AC 10 cm,
C
^
30
°
. Tính A.
A
B
5
3
3
;
B
C
20
3
3
B.
A
B
10
3
3...
Đọc tiếp
Cho tam giác ABC vuông tại A có AC = 10 cm, C ^ = 30 ° . Tính
A. A B = 5 3 3 ; B C = 20 3 3
B. A B = 10 3 3 ; B C = 14 3 3
C. A B = 10 3 3 ; B C = 20 3
D. A B = 10 3 3 ; B C = 20 3 3
Đáp án D
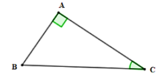
Xét tam giác ABC vuông tại A có
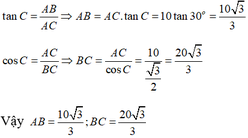
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AC 10 cm,
C
^
30
°
. Tính A.
A
B
5
3
3
;
B
C
20
3
3
B.
A
B
10...
Đọc tiếp
Cho tam giác ABC vuông tại A có AC = 10 cm, C ^ = 30 ° . Tính
A. A B = 5 3 3 ; B C = 20 3 3
B. A B = 10 3 3 ; B C = 14 3 3
C. A B = 10 3 3 ; B C = 20 3
D. A B = 10 3 3 ; B C = 20 3 3
Cho tam giác ABC vuông tại A, có góc C= 30 độ và BC= 100 m. Tính góc ABC
\(\widehat{ABC}=90^0-30^0=60^0\)
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
1. Cho ABC vuông tại A, biết AB = 6cm, góc B = 60∘ . Tính AC, BC.
2. Cho ABC vuông tại A, biết AB = 8cm, góc C = 30∘ . Tính BC, AC.
3. Cho DBC vuông tại D, biết BC = 10cm, góc C = 45∘. Tính BD, DC.
4. Cho ABC vuông tại A có:
a) C= 60 , BC =16. Tính AB, AC.
b)B =45 , BC =5√ 2 . Tính AB, AC.
Cho tam giác ABC vuông tại A,có góc C=30 độ.Trên tia BC lấy điểm M sao cho BM=BA .Tia pg của góc ABC cắt AC tại D. a,c/m:tam giác BAD =tam giác BMD và DM vuông góc với BC b, ABC=?;ADM=? c,Từ C kẻ CH vuông góc với tia BD.C/M: CH // AMgiúp mik nhé,mik đang cần gấp
Xem chi tiết
Cho tam giác ABC vuông tại A có B=2C. Số đo C^ bằng A.110° B.10° C.30° D.20°
cho tam giác ABC vuông tại A, có C=30 độ. cmr : AB= 1/2 BC
Lấy M là trung điểm của BC
Vì tam giác ABC vuông ở A nên B+C=90 độ
Mà C=30 độ nên suy ra góc B=60 độ
Mặt khác tam giác ABC vuông ở A có M là trung điểm của cạnh huyền BC,suy ra MB=MC=1/2BC(1)
Từ đó suy ra tam giác MAB cân ở M và
Theo chứng minh trên B=60 độ
nên suy ra tam giác MAB đều,suy ra AB=MB(2)
Từ (1) và (2) ta được AB=1/2BC
+Trên tia đối AB lấy D/AB = AD
=> A là trung điểm BD
=> AB = 1/2 BD (1)
Xét △ABC,△ADC có :
AB = AD
^CAB = ^CAD = 90o
CA chung
Do đó : △ABC = △ADC (c-g-c)
=> ^DAC = ^BCA ( góc tương ứng)
Mà ^BCA = 30o
=> ^DCA = 30o
Vì A là trung điểm DB
=> A nằm giữa D,B
=> Tia CA nằm giữa CD,CB
=> ^DCA + ^BCA = ^DCB
=> ^DCB = 30 + 30 = 60o
Mà △DCB cân tại C (BC = DC)
=> △DCB đều
=> BD = BC (2)
Từ (1)(2) => AB = 1/2BC
Cho tam giác ABC vuông tại A có BC = 10cm , góc C = 30° .Tính AB,AC,AH,HB
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\Leftrightarrow AB=10\cdot\dfrac{1}{2}=5\left(cm\right)\)
Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
hay \(AC=5\sqrt{3}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=2.5\left(cm\right)\\AH=\dfrac{5\sqrt{3}}{2}\left(cm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có BC=a, CA=b, AB=c. Giải tam giác ABC biết: b=10cm, góc C=30 độ.
Cảm ơn rất nhiều ạ!
Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(\Leftrightarrow AB=10\cdot\dfrac{\sqrt{3}}{3}=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin30^0=\dfrac{AB}{BC}\)
\(\Leftrightarrow BC=\dfrac{10\sqrt{3}}{3}:\dfrac{1}{2}=\dfrac{10\sqrt{3}}{3}\cdot2=\dfrac{20\sqrt{3}}{3}\left(cm\right)\)
Đúng 1
Bình luận (0)