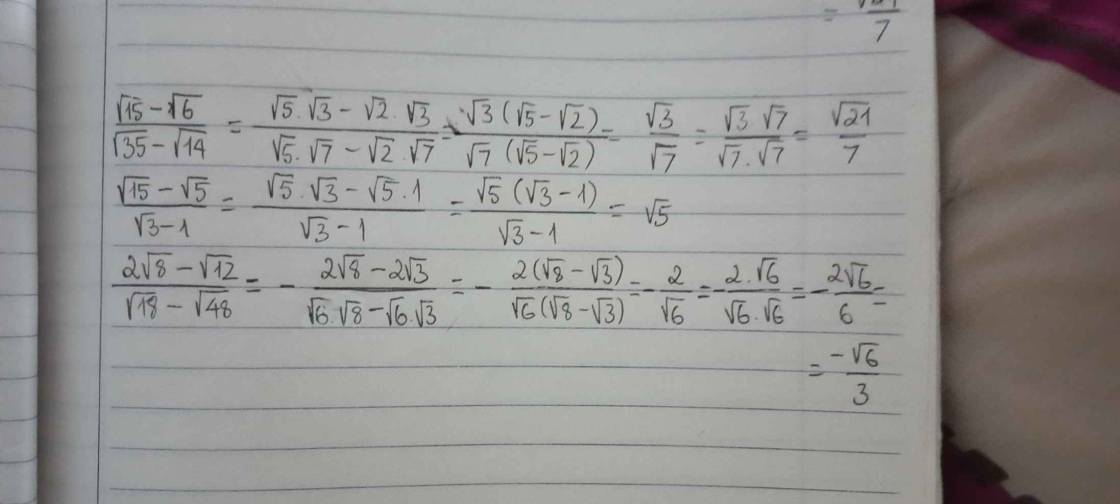\(=\left(3\sqrt{2}-2\sqrt{2}+\sqrt{14}\right).\sqrt{2}-\sqrt{7}\\ =\left(\sqrt{2}+\sqrt{14}\right).\sqrt{2}-\sqrt{7}\\ =2+2\sqrt{7}-\sqrt{7}\\ =2+\sqrt{7}\)

\(\dfrac{\sqrt{15}-\sqrt{6}}{\sqrt{35}-\sqrt{14}}=\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{7}\left(\sqrt{5}-\sqrt{2}\right)}=\sqrt{\dfrac{3}{7}}\)

\(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}=\sqrt{5}\)

\(\dfrac{2\sqrt{8}-\sqrt{12}}{\sqrt{18}-\sqrt{48}}=\dfrac{2\left(\sqrt{8}-\sqrt{3}\right)}{\sqrt{6}\left(\sqrt{3}-\sqrt{8}\right)}=-\dfrac{2\sqrt{6}}{6}\)

`(sqrt 15 - sqrt 6)/(sqrt 35 - sqrt 14)`

`= (sqrt 3 . (sqrt 5 - sqrt 2))/(sqrt 7. (sqrt 5 - sqrt 2))`

`= sqrt3/sqrt 7`

`@ (sqrt 15 - sqrt 5)/(sqrt 3 - 1)`

`= (sqrt 5(sqrt 3 - 1))/(sqrt 3 - 1)`

`= sqrt5`

`@ (2 sqrt 8 - sqrt 12)/(sqrt18 - sqrt 48)`

`= (2(sqrt 8 - sqrt 3)/(sqrt 6(sqrt 3 - sqrt 8))`

`= (-2)/(sqrt 6) = (-2 sqrt 6)/6`

a) 2√18 - 4√50 + 3√32

= 6√2 - 20√2 + 12√2

= -2√2

b) √(√8 - 4)² + √8

= 4 - √8 + √8

= 4

c) √(14 - 6√5) + √(6 + 2√5)

= √(3 - √5)² + √(√5 + 1)²

= 3 - √5 + √5 + 1

= 4

\(a,2\sqrt{18}-4\sqrt{50}+3\sqrt{32}\\ =6\sqrt{2}-20\sqrt{2}+12\sqrt{2}=-2\sqrt{2}\\ b,\sqrt{\left(\sqrt{8}-4\right)^2}+\sqrt{8}\\ =4-\sqrt{8}+\sqrt{8}\\ =4\\ c,\sqrt{14-6\sqrt{5}}+\sqrt{6+2\sqrt{5}}\\ =\sqrt{\left(3+\sqrt{5}\right)^2}+\sqrt{\left(\sqrt{5}+1\right)^2}=3+\sqrt{5}+\sqrt{5}+1\\ =4+2\sqrt{5}\)

`\sqrt(((2-\sqrt5)^2)/8)`

`= (\sqrt((2-\sqrt5)^2))/(\sqrt8)`

`= (|2-\sqrt5|)/(2\sqrt2)`

`=(\sqrt5-2)/(2\sqrt2)`

`=(\sqrt10-2\sqrt2)/4`

.

`7/(3\sqrt14) = (\sqrt7 .\sqrt7)/(3.\sqrt7 .\sqrt2)`

`=(\sqrt7)/(3\sqrt2)`

`=(\sqrt14)/(3.2)`

`=(\sqrt14)/6`

\(\sqrt{\dfrac{\left(2−\sqrt{5}\right)^2}{8}}\)= \(\dfrac{\sqrt{5}-2}{2\sqrt{2}}\)

\(\dfrac{7}{3\sqrt{14}}\) = \(\dfrac{\sqrt{7}}{3\sqrt{2}}\)

\(\sqrt{\dfrac{\left(2-\sqrt{5}\right)^2}{8}}=\dfrac{\sqrt{5}-2}{2\sqrt{2}}=\dfrac{\sqrt{10}-2\sqrt{2}}{4}\)

\(\dfrac{7}{3\sqrt{14}}=\dfrac{7\sqrt{14}}{42}=\dfrac{\sqrt{14}}{6}\)

\(\left(\sqrt{28}-2\sqrt{14}+\sqrt{7}\right)\cdot\sqrt{7}+7\sqrt{8}\)

\(=\left(3\sqrt{7}-2\sqrt{14}\right)\cdot\sqrt{7}+14\sqrt{2}\)

\(=21-14\sqrt{2}+14\sqrt{2}\)

=21

b: Ta có: \(\left(\sqrt{7-3\sqrt{5}}\right)\cdot\left(7+3\sqrt{5}\right)\cdot\left(3\sqrt{2}+\sqrt{10}\right)\)

\(=\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)\left(7+3\sqrt{5}\right)\)

\(=4\left(7+3\sqrt{5}\right)\)

\(=28+12\sqrt{5}\)

Lời giải:

a. 

$A=\sqrt{8+\sqrt{55}}-\sqrt{8-\sqrt{55}}-\sqrt{125}$
$\sqrt{2}A=\sqrt{16+2\sqrt{55}}-\sqrt{16-2\sqrt{55}}-\sqrt{250}$

$=\sqrt{(\sqrt{11}+\sqrt{5})^2}-\sqrt{(\sqrt{11}-\sqrt{5})^2}-5\sqrt{10}$

$=|\sqrt{11}+\sqrt{5}|-|\sqrt{11}-\sqrt{5}|-5\sqrt{10}$

$=2\sqrt{5}-5\sqrt{10}$

$\Rightarrow A=\sqrt{10}-5\sqrt{5}$

b.

$B=\sqrt{7-3\sqrt{5}}.(7+3\sqrt{5})(3\sqrt{2}+\sqrt{10})$

$B\sqrt{2}=\sqrt{14-6\sqrt{5}}(7+3\sqrt{5})(3\sqrt{2}+\sqrt{10})$

$=\sqrt{(3-\sqrt{5})^2}(7+3\sqrt{5}).\sqrt{2}(3+\sqrt{5})$

$=(3-\sqrt{5})(7\sqrt{2}+3\sqrt{10})(3+\sqrt{5})$

$=(3^2-5)(7\sqrt{2}+3\sqrt{10})$

$=4(7\sqrt{2}+3\sqrt{10})=28\sqrt{2}+12\sqrt{10}$

$\Rightarrow B=28+12\sqrt{5}$

c.

$C=\sqrt{2}(\sqrt{7}-\sqrt{5})(6-\sqrt{35})\sqrt{6+\sqrt{35}}$

$=(\sqrt{7}-\sqrt{5})(6-\sqrt{35})\sqrt{12+2\sqrt{35}}$

$=(\sqrt{7}-\sqrt{5})(6-\sqrt{35})\sqrt{(\sqrt{7}+\sqrt{5})^2}

$=(\sqrt{7}-\sqrt{5})(6-\sqrt{35})(\sqrt{7}+\sqrt{5})$

$=(7-5)(6-\sqrt{35})$

$=2(6-\sqrt{35})=12-2\sqrt{35}$

a) \(\frac{\sqrt{6}+\sqrt{14}}{2\sqrt{3}+\sqrt{28}}=\frac{\sqrt{6}+\sqrt{14}}{\sqrt{2}\left(\sqrt{6}+\sqrt{14}\right)}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\)

b) \(\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+\sqrt{16}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=\frac{\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)+\sqrt{2}\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)

\(\frac{\left(\sqrt{2}+1\right)\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=\sqrt{2}+1\)

\(\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+\sqrt{16}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=\frac{\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)+\left(\sqrt{4}+\sqrt{6}+\sqrt{8}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)

\(=\frac{\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)+\sqrt{2}\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=\frac{\left(1+\sqrt{2}\right)\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=1+\sqrt{2}\)