Câu hỏi của vuighe123_oribe - Toán lớp 8 - Học toán với OnlineMath

gọi thương khi chia đa thức A cho x + y + z là Q, ta có :

x³ + y³ + z³ + kxyz = ( x + y + z ) . Q

đẳng thức trên đúng với mọi x,y,z nên với x = 1, y = 1, z = -2 ta có :

1 + 1 + ( -2 )³ + k . ( -2 ) = ( 1 + 1 - 2 ) . Q \(\Rightarrow\)-6 - 2k = 0 \(\Rightarrow\)k = -3

với k = -3 ta có : x³ + y³ + z³ - 3xyz chia hết cho x + y + z ( thương là x² + y² + z² - xy - yz - zx )

Vậy ...

gọi thương khi chia đa thức A cho x + y + z là Q ta có

x^3 =y^3+z^3 +kxyzz =(x + y +z) .Q

đẳng thức trên có thể đúng với các chữ như x,y,z nên x = 1y , 1z = -2 

nên : 

=>k = - 3 ta cs : x^ +y^3 +z^3 - 3xyz chia hết cho x =y +z (thườn là x2 + y2 -xy - z - zx)

Xem lại đề

Xem A là một đa thức theo x, kí hiệu \(A(x)\)

Vì \((x+y+z)=x-(-y-z)\)và \(A⋮(x+y+z)\)nên \(A(x)⋮\left[x-(-y-z)\right]\)

Suy ra \(A(-y-z)=0\Leftrightarrow(-y-z)^3+y^3+z^3+k(-y-z)yz=0\)

\(\Leftrightarrow-3yz(y+z)+k(-y-z)yz=0\Leftrightarrow-yz(y+z)(3+k)=0\)

Đẳng thức trên đúng \(\forall y,z\Leftrightarrow k=-3\)

\(A=x^3+y^3+z^3+kxyz\)

Thực hiện phép chia ta được

\(A=\left(x^3+y^3+z^3+kxyz\right)\div\left(x+y+z\right)\)

\(A=\left(x+y+z\right)\left[x^2+y^2+z^2-xy-xz-yz-yz\left(k+2\right)\right]-yz\left(x+z\right)\left(k+3\right)\)

Để phép chia hết thì: \(yz\left(x+z\right)\left(k+3\right)=0\)

Suy ra:
Suy ra: \(k=3\)

k = -3

Xin lỗi đáp án là âm 3, mình biết bị thíu

Bài 3:

a, (\(x\)+y+z)²

=((\(x\)+y) +z)²

= (\(x\) + y)² + 2(\(x\) + y)z + z²

= \(x^2\) + 2\(xy\) + y² + 2\(xz\) + 2yz + z²

=\(x^2\) + y² + z² + 2\(xy\) + 2\(xz\) + 2yz

b, (\(x-y\))(\(x^2\) + y² + z² - \(xy\) - yz - \(xz\))

= \(x^3\) + \(xy^2\) + \(xz^2\) - \(x^2\)y - \(xyz\) - \(x^2\)z - y³ 

Đến dây ta thấy xuất hiện \(x^3\) - y³ khác với đề bài, em xem lại đề bài nhé

c,

(\(x\) + y + z)³ 

=(\(x\) + y)³ + 3(\(x\) + y)²z + 3(\(x\)+y)z² + z³

= \(x^3\) + 3\(x^2\)y + 3\(xy^{2^{ }}\) + y³ +  3(\(x\)+y)z(\(x\) + y + z) + z³

= \(x^3\) + y³ + z³ + 3\(xy\)(\(x\) + y) + 3(\(x+y\))z(\(x+y+z\))

= \(x^3\) + y³ + z³ + 3(\(x\) + y)( \(xy\) + z\(x\) + yz + z²)

= \(x^3\) + y³ + z³ + 3(\(x\) + y){(\(xy+xz\)) + (yz + z²)}

= \(x^3\) + y³ + z³ + 3(\(x\) + y){ \(x\)( y +z) + z(y+z)}

= \(x^3\) + y³ + z³ + 3(\(x\) + y)(y+z)(\(x+z\)) (đpcm)

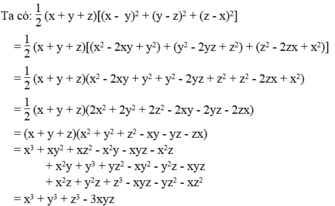
Vế trái bằng vế phải nên đẳng thức được chứng minh.

Nếu x ≥ 0, y  ≥  0, z  ≥  0 thì:

x + y + z  ≥  0

x - y 2 + y - z 2 + z - x 2 ≥ 0

Suy ra:

x 3 + y 3 + z 3 - 3 x y z ≥ 0 ⇔ x 3 + y 3 + z 3 ≥ 3 x y z

Hay:  x 3 + y 3 + z 3 3 ≥ x y z

Áp dụng bđt AM - GM:

\(x^3+1+1\ge3x;y^3+1+1\ge3y;z^3+1+1\ge3z;2x+2y+2z\ge6\sqrt[3]{xyz}=6\).

Cộng vế với vế các bđt trên rồi rút gọn ta có đpcm.

Áp dụng BĐT Cosi:

\(\left(x^3+1+1\right)+\left(y^3+1+1\right)+\left(z^3+1+1\right)\)

\(\ge3\left(x+y+z\right)\)

\(\ge x+y+z+2.3\sqrt[3]{xyz}\)

\(=x+y+z+6\)

\(\Rightarrow x^3+y^3+z^3\ge x+y+z\)

Đẳng thức xảy ra khi \(x=y=z=1\)

Ta rút gọn tử thức trc: \(x^3+y^3+z^3-3xyz=x^3+y^3+z^3+x^2y-x^2y+xy^2-xy^2+y^2z-y^2z+yz^2-yz^2+x^2z-x^2z+xz^2-xz^2-xyz-xyz-xyz=x^2\left(x+y+z\right)+y^2\left(x+y+z\right)+z^2\left(x+y+z\right)-x\left(x+y+z\right)-yz\left(x+y+z\right)-xz\left(x+y+z\right)=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)=\frac{1}{2}\left(x+y+z\right)\left(x^2-2xy+y^2+y^2-2yz+z^2+z^2-2xz+x^2\right)=\frac{1}{2}\left(x+y+z\right)\left(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right)\)tới đây rút gọn đc rồi chứ

Lời giải:
Ta sử dụng các công thức hằng đẳng thức đáng nhớ:

\(A=x^3+y^3+z^3+kxyz=(x+y)^3-3xy(x+y)+z^3+kxyz\)

\(=(x+y)^3+z^3-3xy(x+y)+kxyz\)

\(=(x+y+z)^3-3(x+y)z^2-3(x+y)^2z-3xy(x+y)+kxyz\)

\(=(x+y+z)^3-3(x+y)z(z+x+y)-3xy(x+y+z)+(k+3)xyz\)

\(=(x+y+z)^3-3(x+y+z)(xy+yz+xz)+(k+3)xyz\)

\(=(x+y+z)(x^2+y^2+z^2-xy-yz-xz)+(k+3)xyz\)

Vậy để \(A\vdots x+y+z\) thì \((k+3)xyz\vdots x+y+z, \forall x,y,z\)

Điều này xảy ra chỉ khi \(k+3=0\Leftrightarrow k=-3\)