cho tam giác ABC có AB=10cm,AC=17cm,BC=15cm, tính diện tích tam giác ABC

Những câu hỏi liên quan
Cho tam giác ABC có AB = 10cm; AC=17cm; BC=21cm. Kẻ AH vuông góc với BC. Tính: HC, HB, AH và diện tích tam giác ABC
Cho tam giác ABC, có cạnh AB 15cm, canh AC 20cm. Trên cạnh AB lấy điểm M sao cho AM 10cm, trên cạnh AC lấy điểm E sao cho AE 15cm. Nối điểm M với E. Tính diện tích tam giác ABC, biết diện tích tam giác AME là 34,8cm2.
Đọc tiếp
Cho tam giác ABC, có cạnh AB =15cm, canh AC = 20cm. Trên cạnh AB lấy điểm M sao cho AM =10cm, trên cạnh AC lấy điểm E sao cho AE = 15cm. Nối điểm M với E. Tính diện tích tam giác ABC, biết diện tích tam giác AME là 34,8cm2.
Cho tam giác ABC có cạnh AB = 15cm, cạnh AC bằng 20cm. Trên cạnh AB lấy điểm M sao cho AM = 10cm, trên cạnh AC lấy điểm E sao cho AE = 15cm. Nối điểm M với điểm E. Tính diện tích tam giác ABC, biết diện tích tam giác AME là 34,8cm2. Diện tích tam giác ABC là:
Ta nối E với B để được tam giác AEB
Diện tích của tam giác AEB là:
34,8 : 2 x 3 = 52,2 cm²
Diện tích của tam giác ABC là:
52,2 : 3 x 4 = 69,6 cm²
k nhé
câu hỏi đấy j
Xem thêm câu trả lời
Cho tam giác ABC có AB=10cm, AC=17cm, BC=21cm và đường cao AH.
a. Tính AH
b. Tính các góc của tam giác ABC
Cho tam giác ABC có AB =15cm AC =20cm trên cạnh AB lấy điểm D sao cho AD bằng 10cm trên cạnh AC lấy điểm E sao cho AE =15cm nối D với E tính diện tích tam giác ABC biết diện tích tam giác ADE =45cm2
Mình biểu diễn bằng hình vẽ trên.
Xét EAD và EDB chung đỉnh E, đáy AD gấp 2 lần đáy DB (10 : (15 -10) = 2)
=> S_EAD gấp 2 lần S_EDB => Diện tích EDB = 45 : 2 = 22,5 (cm2)
Diện tích BAE là : 45 + 22,5 = 67,5 (cm2)
Xét tam giác BAE và tam giác AEC có chung đỉnh B và đáy AE gấp 3 lần đáy EC (15 : (20-15) = 3)
=> Diện tích BAE gấp 3 lần diện tích AEC. Vậy diện tích AEC là : 67,5 : 3 =22,5 (cm2)
Vậy diện tích ABC là : 67,5 + 22,5 = 90 (cm2)
Cho tam giác ABC có AB=15cm, AC=20cm,BC=25cm. Đường phân giác góc BAC cắt BC tại D
a) tính độ dài DB và DC
b) tính tỉ số diện tích tam giác ABC và tam giác ACD
c)Cho tam giác ABC có diện tích bằng F tính diện tích tam giác ABD và diện tích tam giác ACD theo F
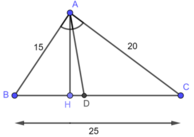
a) Trong tam giác ABC, ta có: AD là đường phân giác của:
⇒\(\dfrac{DB}{DC}\)=\(\dfrac{AB}{AC}\)
Mà AB = 15cm và AC = 20cm ( gt )
Nên \(\dfrac{DC}{DB}\)=\(\dfrac{15}{20}\)
⇒\(\dfrac{DB}{DB+DC}\)=\(\dfrac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )
⇒\(\dfrac{DB}{BC}\)=\(\dfrac{15}{35}\)⇒DB=\(\dfrac{15}{35}\).BC=\(\dfrac{15}{35}\).25=\(\dfrac{75}{5}\)(cm)
b) Kẻ AH⊥BC
Ta có:\(S_{ABD}\)=\(\dfrac{1}{2}\)AH.BD
\(S_{ACD}\)=\(\dfrac{1}{2}\)AH.CD
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.CD}\)=\(\dfrac{BD}{DC}\)
Mà \(\dfrac{DB}{DC}\)=\(\dfrac{15}{12}\)=\(\dfrac{3}{4}\)
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{3}{4}\)(đpcm)
Đúng 0
Bình luận (0)
cho tam giác ABC có BC=15cm , đường cao AH=10cm . ! đường thẳng d song song với BC cắt AB,AC theo thứ tự DE. a) Tính diện tích ABC
Cho tam giác ABC có AB=17cm, AC=15cm, BC=8cm.
a) Chứng minh: tam giác ABC vuông.
b) vẽ đường cao CK của tam giác ABC. Giải tam giác vuông BKC
a) Xét tam giác ABC có:
\(AC^2+BC^2=225+64=289=AB^2\)
Nên tam giác ABC vuông tại A.
b) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông, ta được:
\(CK=\dfrac{AC\cdot BC}{AB}=\dfrac{15\cdot8}{17}=\dfrac{120}{17}\left(cm\right)\\BK=\dfrac{BC^2}{AB}=\dfrac{64}{17}\left(cm\right)\)
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta được:
\(\sin B=\dfrac{CK}{BC}=\dfrac{15}{17}\\ \Rightarrow\widehat{B}\approx62^0\)
\(\sin C=\dfrac{BK}{BC}=\dfrac{8}{17}\\ \Rightarrow\widehat{C}\approx28^0\)
Đúng 1
Bình luận (0)
a: Xét ΔABC có \(AB^2=AC^2+BC^2\)
nên ΔBAC vuông tại C
Đúng 0
Bình luận (0)
Cho tam giác ABC biết cạnh AB =15cm , cạnh AC= 17cm và chu vi tam giác=41 cm Hãy tính cạnh BC
Độ dài cạnh BC là:
41 - ( 15 + 17) = 9 (cm)
Kết luận:..
Đúng 1
Bình luận (0)



















