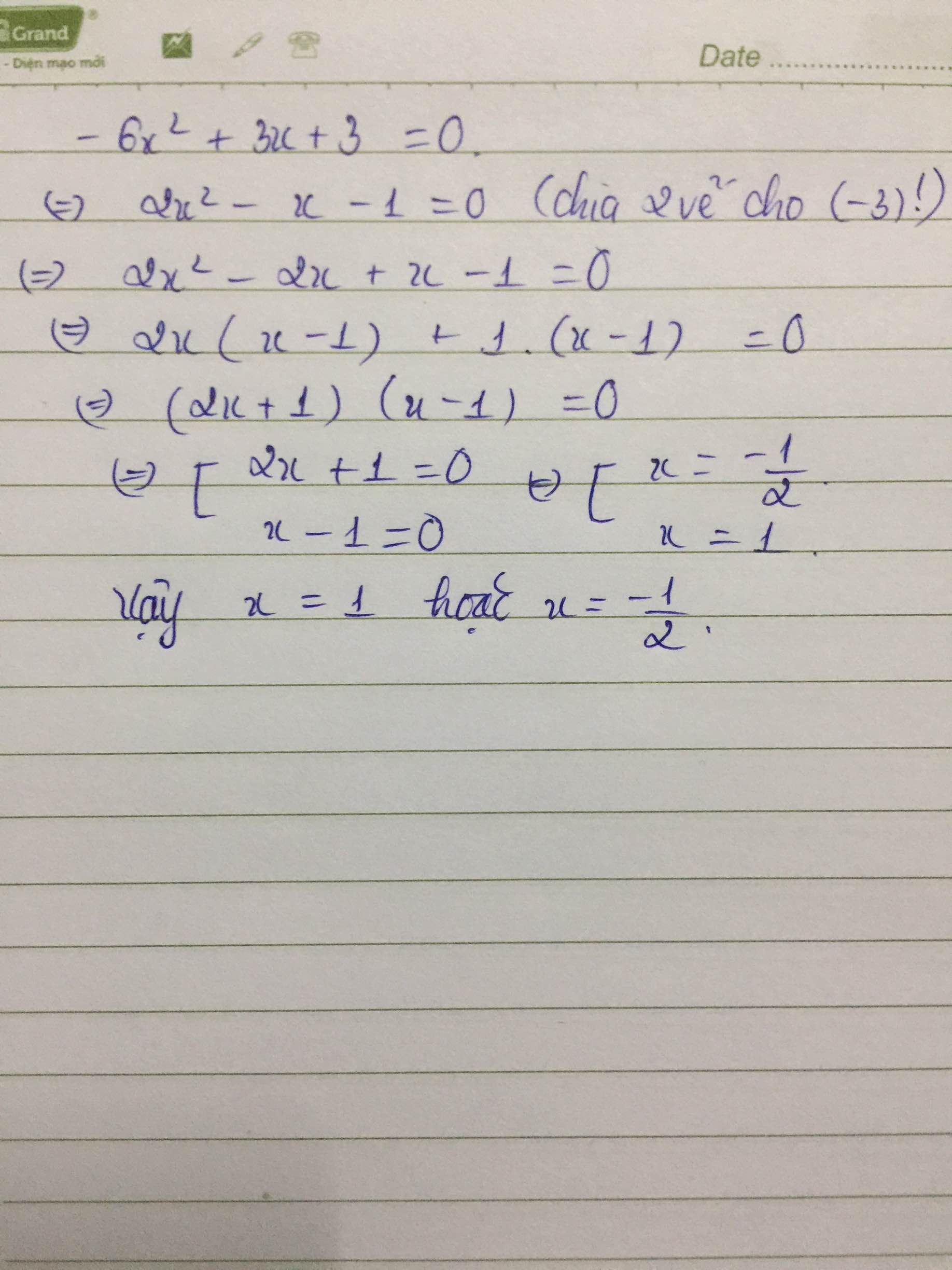tìm nghiệm của đa thức 1x+3x^2 hoặc chứng minh đa thức vô nghiệm

Những câu hỏi liên quan
Tìm nghiệm hoặc cm đa thức vô nghiệm
-6x^2+3x+3
chứng minh đa thức vô nghiệm -3x^2+x-2
\(-3x^2+x-2=-3\left(x^2-\frac{1}{3}x+\frac{2}{3}\right)\)
\(=-3\left(x^2-2.x.\frac{1}{6}+\frac{1}{36}-\frac{1}{36}+\frac{2}{3}\right)\)
\(=-3\left[\left(x-\frac{1}{6}\right)^2+\frac{23}{36}\right]=-3\left(x-\frac{1}{6}\right)^2-\frac{23}{12}\)
Đa thức luôn âm \(\Rightarrow\)phương trình vô nghiệm
Đúng 0
Bình luận (0)
\(-3x^2+x-2=-3\left(x^2-\frac{1}{3}x+\frac{2}{3}\right)\)
\(=-3\left(x^2-2x.\frac{1}{6}+\frac{1}{36}-\frac{1}{36}+\frac{2}{3}\right)\)
\(=-3\left[\left(x-\frac{1}{6}\right)^2+\frac{23}{36}\right]\)
\(=-3\left(x-\frac{1}{6}\right)^2-\frac{23}{12}\)
=> Phương trình luôn vô nghiệm
Đúng 0
Bình luận (0)
1. Chứng minh đa thức C(x)= x^2 + 4x + 2014 vô nghiệm
2. Tìm nghiệm của đa thức D(x)= (x-2)^2 - (x-2).(-x+1)
cho đa thức p(x)=-8x^3+3x^4-x^2+5x^2-2020+6x^3-3x^4+2025+2x^3 chứng minh đa thức p(x) vô nghiệm
P(x)=-8x^3+6x^3+2x^3+3x^4-3x^4+4x^2-2020+2025
=4x^2+5>=5>0 với mọi x
=>P(x) không có nghiệm
Đúng 0
Bình luận (1)
chứng minh đa thức x2-3x+3 vô nghiệm
x^2 - 3x + 3
=x^2 - 1,5x - 1,5x + 2,25+0,75
=x(x-1,5)-1,5(x-1,5)+0,75
=(x-1,5)^2 + 0,75 >= 0,75 => vô nghiệm
Đúng 0
Bình luận (0)
cho đa thức : h(x) = x^4 + 1/2x^2 + 2012 . chứng tỏ h(x) vô nghiệm
CTR đa thứa : 3x^2010 + x^1002+ 1 vô nghiệm
CTR đa Thức : M(x)= x^2 + 2x + 2 vô nghiệm
CTR đa thức : M(x) = x^2 + 2x + 1 chỉ có 1 nghiệm duy nhất tìm nghiệm duy nhất đó
CMR đa thức M(x) = x^2 - x + 5 không có nghiệm nguyên
chứng minh rằng đa thức: x^2-3x+12 vô nghiệm với mọi x
vì x^2 >hoặc= 0 (với mọi giá trị của x)
Suy ra x^2-3x+12 > 0 (với mọi x)
Suy ra x^2-3x+12 khác o
Suy ra x^2-3x+12 vô nghiệm
Đúng 0
Bình luận (0)
Tham khảo:x^2-5x+20
ta có: x^2-5x+20=x^2-2/5x-2/5x+25/4-25/4+20
=(x^2-2/5x)-(2/5x-25/4)-25/4+80/4
=x(x-2/5)-2/5(x-2/5)+55/4
=(x-2/5)(x-2/5)+55/4
=(x-2/5)^2+55/4
Ta có: (x-2/5)^2>=0 Với x thuộc R
(x-2/5)^2+55/4>=55/4>0
=>Đa thức không có nghiệm
Đúng 0
Bình luận (0)
tìm nghiệm của đa thức f(x) : 3x^2+1x
3x2+x=0
<=>3x(x+1)=0
<=>3x=0 hoặc x+1=0
<=>x=0 hoặc x=-1
Đúng 0
Bình luận (0)
f(x)=3x^2+1x
=3x^2+x
=x(3x+1)=0
\(\Rightarrow\)x=0 hoặc 3x+1=0
\(\Rightarrow\orbr{\begin{cases}x=0\\x=-\frac{1}{3}\end{cases}}\)
vậy x=0; x=-1/3 là nghiệm của đa thức f(x)
Đúng 0
Bình luận (0)
chứng minh đa thức sau vô nghiệm: 3x2-6x+15
ta có :\(^{3x^2-6x\ge0}\)
15 >0
=}\(^{3x^2-6x+15\ge15}\)
=}đa thức \(3x^2-6x+15\)vô nghiệm
k giùm mình nhé
Đúng 0
Bình luận (0)
=(3x2-3x)-(3x+3)+12
=3x(x-1)-3(x-1)+12
=(x-1)(3x-3)+12
=(x-1).3.(x-1)+12
=3.(x-1)2+12
Ta có: 3.(x-1)2\(\ge\)0,\(\forall x\)12>0
=>3(x-1)2+12>0
Vậy đa thức trên vô nghiệm
Đúng 0
Bình luận (0)