Tập hợp các nghiệm của đa thức f(x)= x3+x2+x+1 có số phần tử là/
HELP ME, PLEASE
Bài 1: Cho đa thức f(x) = x2 + 4x - 5
a) Số -5 có phải là nghiệm của f(x) không?
b) Viết tập hợp S tất cả các nghiệm của f(x)
a: \(f\left(-5\right)=\left(-5\right)^2+4\cdot\left(-5\right)-5=0\)
=>x=-5 là nghiệm của f(x)
b: S={-5;1}
Cho 2 đa thức : f(x) = -2x2 - 3x3 - 5x + 5x3 - x + x2 + 4x + 3 + 4x2
g(x) = 2x2 - x3 + 3x + 3x3 + x2 - x - 9x + 2
a) Tìm h(x) = f(x) - g(x)
b) Tìm nghiệm của đa thức h(x)
HELP ME!!!THANKS CÁC CẬU NHIỀU LẮM Ạ!!
h(x)=5x+1
nghiệm_của_đa_thức_h(x)_là_-1/5
Cho 2 đa thức : f(x) = -2x2 - 3x3 - 5x + 5x3 - x + x2 + 4x + 3 + 4x2
g(x) = 2x2 - x3 + 3x + 3x3 + x2 - x - 9x + 2
a) Tìm h(x) = f(x) - g(x)
b) Tìm nghiệm của đa thức h(x)
HELP ME!!!THANKS CÁC CẬU NHIỀU LẮM Ạ!!
a)h(x)=f(x)-g(x)
=(2x3 +3x2 -2x +3)-(2x3 +3x2 -7x +2)
=2x3 + 3x2 - 2x +3 - 2x3 -3x2 + 7x -2
=5x+1
b)h(x)=5x+1=0
=>5x=-1
x=\(\frac{-1}{5}\)
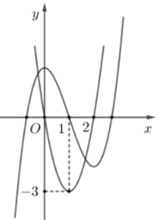
Cho hàm số đa thức bậc ba y=f(x) có đồ thị của các hàm số y=f(x), y=f '(x)như hình vẽ bên.Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(f(x)-m)+2f(x)=3(x+m) có đúng 3 nghiệm thực .Tổng các phần tử của S bằng
A. 0
B. -6
C. -7
D. -5
Ta có ![]()
![]()
Quan sát đồ thị có 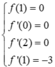
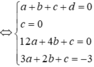

![]()
Đặt ![]() phương trình trở thành:
phương trình trở thành:
![]()
![]()
![]()
Khi đó ![]()
Phương trình này có 3 nghiệm phân biệt
![]()
Tổng các phần tử củaS bằng 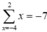
Chọn đáp án C.
Cho 2 đa thức : f(x) = -2x2 - 3x3 - 5x + 5x3 - x + x2 + 4x + 3 + 4x2
g(x) = 2x2 - x3 + 3x + 3x3 + x2 - x - 9x + 2
a) Tìm h(x) = f(x) - g(x)
b) Tìm nghiệm của đa thức h(x)
HELP ME!!!THANKS CÁC CẬU NHIỀU LẮM Ạ!!
a) Tìm h(x) = f(x) - g(x)
f(x) - g(x) = (-2x2 - 3x3 - 5x + 5x3 - x + x2 + 4x + 3 + 4x2) - (2x2 - x3 + 3x + 3x3 + x2 - x - 9x + 2)
= -2x2 - 3x3 - 5x + 5x3 - x + x2 + 4x + 3 + 4x2 - 2x2 + x3 - 3x - 3x3 - x2 + x + 9x - 2
= (-2x2 + x2 + 4x2 - 2x2 - x2) + (-3x3 + 5x3 + x3 - 3x3) + (-5x - x + 4x - 3x + x + 9x) + (3 - 2)
= 5x + 1
Vậy h(x) = 5x + 1
b) Tìm nghiệm của đa thức h(x)
Cho h(x) = 0
\(\Leftrightarrow\) 5x + 1 = 0
5x = 0 + 1
5x = 1
x = \(\dfrac{1}{5}\)
Vậy x = \(\dfrac{1}{5}\) là nghiệm của đa thức h(x).
1. Cho đa thức f(x)ϵZ[x]f(x)ϵZ[x]
f(x)=ax4+bx3+cx2+dx+ef(x)=ax4+bx3+cx2+dx+e với a, b, c, d, e là các số lẻ.
Cm đa thức không có nghiệm hữu tỉ
2. Cho P(x) có bậc 3; P(x)ϵZ[x]P(x)ϵZ[x] và P(x) chia hết cho 7 với mọi x ϵZϵZ
CmR các hệ số của P(x) chia hết cho 7.
3. Cho đa thức P(x) bậc 4 có hệ số cao nhất là 1 thỏa mãn P(1)=10; P(2)=20; P(3)=30.
Tính P(12)+P(−8)10P(12)+P(−8)10
4. Tìm đa thức P(x) dạng x5+x4−9x3+ax2+bx+cx5+x4−9x3+ax2+bx+c biết P(x) chia hết cho (x-2)(x+2)(x+3)
5. Tìm đa thức bậc 3 có hệ số cao nhất là 1 sao cho P(1)=1; P(2)=2; P(3)=3
6. Cho đa thức P(x) có bậc 6 có P(x)=P(-1); P(2)=P(-2); P(3)=P(-3). CmR: P(x)=P(-x) với mọi x
7. Cho đa thức P(x)=−x5+x2+1P(x)=−x5+x2+1 có 5 nghiệm. Đặt Q(x)=x2−2.Q(x)=x2−2.
Tính A=Q(x1).Q(x2).Q(x3).Q(x4).Q(x5)A=Q(x1).Q(x2).Q(x3).Q(x4).Q(x5) (x1,x2,x3,x4,x5x1,x2,x3,x4,x5 là các nghiệm của P(x))
Bài: a) Xác định đa thức f(x) = ax + b biết f(2) = - 4 ; F(3) = 5.
b) Xác định a và b biết nghiệm của đa thức G(x) = x2 – 1 là nghiệm của đa thức Q(x) = x3 + ax2 + bx – 2
Cho g(x) là 1 đa thức với hệ số nguyên. CM: Đa thức f(x)=x2+x.g(x3)f(x)=x2+x.g(x3) không chia hết cho đa thức: x2−x+1
Cho 2 đa thức:
f(x) = x2 - 6x + 5 và h(x) = x4 + 1/5.x2 + 2012
a. Trong tập hợp số { 5; 3; -1;0} số nào là nghiệm số nào không là nghiệm của đa thức
b. Hãy viết tập hợp S tất cả các nghiệm của f(x)
c. Hãy c/m đa thức h(x) không có nghiệm
Giúp mik với
a) ta có:
+) x = 5 => f(5) = 52 - 6.5 + 5 = 25 - 30 + 5 = 0
=> x = 5 là nghiệm của f(x)
+) x = 3 => f(3) = 32 - 6.3 + 5 = 9 - 18 + 5 = -4
=> x = 3 ko là nghiệm của f(x)
+) x = 1 =. f(1) = 12 - 6.1 + 5 = 1 - 6 + 5 = 0
=> x = 1 là nghiệm của f(x)
+) x = 0 => f(0) = 02 - 6.0 + 5 = 5
=> x = 5 ko là nghiệm của f(x)
b) Tập hợp S = {5; -1}
c) Ta có : x4 \(\ge\)0 ; 1/5x2 \(\ge\)0 ; 2012 > 0
=> x4 + 1/5x2 + 2012 > 0
=> đa thức h(x) ko có nghiệm
\(a.\)Thay lần lượt các giá trị của \(x\)trong tập hợp số \(\left\{5;3;-1;0\right\}\)vào đa thức \(f\left(x\right)\)như bn Edogawa Conan nha !
Ta thấy \(f\left(5\right)=5^2-6.5+5=0\)nên \(x=5\)là 1 ngiệm của \(f\left(x\right)\)
\(b.\)Ta có: \(f\left(x\right)=x^2-x-5x+5=x\left(x-1\right)-5\left(x-1\right)=\left(x-1\right)\left(x-5\right)\)
\(f\left(x\right)=0\Leftrightarrow\cdot x-1\left(x-5\right)=0\Leftrightarrow\orbr{\begin{cases}x=1\\x=5\end{cases}}\)
\(c.\)Xét đa thức \(h\left(x\right)=x^4+\frac{1}{5}x^2+2012\)
Do \(x^4\ge0\)và \(\frac{1}{5}x^2\ge0\)với mọi \(x\)nên \(h\left(x\right)>0\)với mọi \(x\)
Vậy \(h\left(x\right)\ne0\)với mọi \(x\)Do đó đa thức \(h\left(x\right)\)không có nghiệm