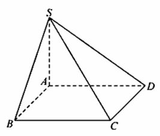
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và S A ⊥ A B C D , S A = x . Xác định x để hai mặt phẳng (SBC) và (SDC) tạo với nhau một góc bằng 60 °
A. x = a 3
B. x = a
C. x = a 3 2
D. x = a 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và S A ⊥ A B C D , S A = x . Xác định x để hai mặt phẳng (SBC) và (SDC) tạo với nhau một góc bằng 60 °

A. x = a 3
B. x = a
C. x = a 3 2
D. x = a 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, S A ⊥ A B C D , S A = x . Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60 °
A. x = 3 a 2 .
B. x = a 2 .
C. x = a
D. x = 2a
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, S A ⊥ A B C D , S A = x . Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60 ° .
A. x = 3 a 2 .
B. x = a 2 .
C. x = a .
D. x = 2 a .
Đáp án C
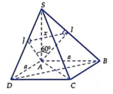
+ Trong S A B dựng A I ⊥ S B ta chứng minh được A I ⊥ S B C 1 .
Trong S A D dựng A J ⊥ S D ta chứng minh được A J ⊥ S C D 2 .
Từ (1) và (2) ⇒ S B C , S C D ^ = A I , A J ^ = I A J ^
+ Ta chứng minh được A I = A J . Do đó, nếu góc I A J ^ = 60 ° thì Δ A I J đều ⇒ A I = A J = I J .
Δ S A B vuông tại A có AI là đường cao ⇒ A I . S B = S A . A B ⇒ A I = S A . A B S B 3
Và có S A 2 = S I . S B ⇒ S I = S A 2 S B 4
Ta chứng minh được I J // B D ⇒ I J B D = S I S B ⇒ I J = S I . B D S B = 4 S A 2 . B D 2 S B 2 5 .
Thế (3)&(5) vào A I = I J ⇒ A B = S A . B D S B ⇔ A B . S B = S A . B D .
⇔ a . x 2 + a 2 = x . a 2 ⇔ x 2 + a 2 = 2 x 2 ⇔ x = a
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. Biết AB=2a, AD=DC=a. Cạnh bên SA vuông góc với đáy và \(SA=a\sqrt{2}\). CHọn khẳng định sai?
A: \(\widehat{\left(SBC\right);\left(ABCD\right)}=45^0\)
B: \(\widehat{\left(SDC\right);\left(BCD\right)}=60^0\)
C: Giao tuyến của (SAB) với (SCD) song song AB
D: \(\left(SBC\right)\perp\left(SAC\right)\)
B là khẳng định sai
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(CD=\left(SCD\right)\cap\left(BCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SDC) và (BCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{2}\Rightarrow\widehat{SDA}\approx54^044'\)
Cho hình chóp S.ABCD có \(SA\perp\left(ABCD\right)\), đáy ABCD là hình vuông cạnh 2a, SA= \(2a\sqrt{3}\) .
1. Chứng minh \(\left(SAC\right)\perp\left(SBD\right)\)
2. Gọi I là trung điểm của AD, mặt phẳng (P) qua I và vuông góc với SD. Xác định và tính thiết diện của hình chóp cắt bởi mặt phẳng (P).
Help me!!!
1: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SAC) vuông góc (SBD)
Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, có AB = 2a, AD = DC = a, có cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a
a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB)
b) Gọi \(\varphi\) là góc giữa hai mặt phẳng (SBC) và (ABCD), tính \(\tan\varphi\)
c) Gọi \(\left(\alpha\right)\) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định \(\left(\alpha\right)\) và xác định thiết diện của hình chóp S.ABCD với \(\left(\alpha\right)\)
Cho hình chóp S.ABCD có SA vuông góc (ABCD), ABCD là hình chữ nhật. AB=a, \(AD=a\sqrt{3}\). Biết rằng mp(SDC) tạo với đáy một góc bằng 60 độ.
a. Tính \(cos\left(\widehat{\left(SBC\right);\left(ABCD\right)}\right)\)
b: Tính \(tan\left(\widehat{\left(SBD\right);\left(ABCD\right)}\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà CD là giao tuyến (SCD) và (ABCD)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(\Rightarrow\widehat{SDA}=60^0\Rightarrow SA=AD.tan60^0=3a\)
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABCD)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=3\Rightarrow\widehat{SBA}=...\)
b.
Từ A kẻ \(AE\perp BD\)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\)
\(\Rightarrow BD\perp\left(SAE\right)\Rightarrow\widehat{SEA}\) là góc giữa (SBD) và (ABCD)
Hệ thức lượng: \(\dfrac{1}{AE^2}=\dfrac{1}{AB^2}+\dfrac{1}{AD^2}\Rightarrow AE=\dfrac{a\sqrt{3}}{2}\)
\(tan\widehat{SEA}=\dfrac{SA}{AE}=2\sqrt{3}\Rightarrow\widehat{SEA}=...\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. S A ⊥ A B C D , S A = x . Xác định x để 2 mặt phẳng (SBC) và (SCD) hợp với nhau một góc 60 °
A. x = 2a
B. x = a
C. x = 3 a 2
D. x = a 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ⊥ (ABCD), SA = x. Tìm x để hai mặt phẳng (SBC) và (SCD) tạo với nhau một góc 60 ° .
A. x = 2 a
B. x = 3 a 2
C. x = a 2
D. x = a
Chọn D.
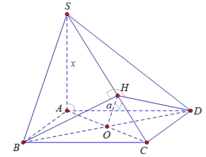
- Kẻ BH ⊥ SC ⇒ DH ⊥ SC (hai đường cao tương ứng của hai tam giác bằng nhau).
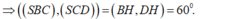
- Có 2 trường hợp xảy ra:
TH1:
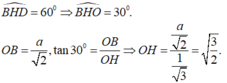
- Xét hai tam giác đồng dạng SAC và OHC ta có

TH2:
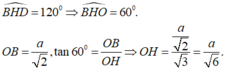
- Xét hai tam giác đồng dạng SAC và OHC ta có:
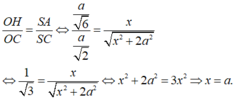
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\) ,\(SA=a\) và vuông góc với đáy \(\left(ABCD\right)\) .Gọi \(M\) là trung điểm của \(BC\).Tính cosin của góc giữa hai mặt phẳng \(\left(SMD\right)\) và \(\left(ABCD\right)\).