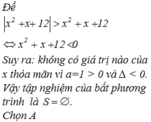\(\Leftrightarrow\left\{{}\begin{matrix}8-x\ge0\\x-2\ge0\\8-x\le\left(x-2\right)^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2\le x\le8\\x^2-3x-4\ge0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2\le x\le8\\\left[{}\begin{matrix}x\ge4\\x\le-1\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow4\le x\le8\)

x=\(\left\{{}\begin{matrix}x=3\\x=-3\\x=-2\end{matrix}\right.\)

\(\Rightarrow\) (-\(\infty\); -3] \(\cup\) { 3 }

2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)

Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)

TXĐ: \(x>-4\)

Khi đó BPT tương đương:

\(x^2+2x>3\Leftrightarrow x^2+2x-3>0\)

\(\Rightarrow\left[{}\begin{matrix}x>1\\x< -3\end{matrix}\right.\)

Vậy tập nghiệm của BPT là: \(\left[{}\begin{matrix}x>1\\-3< x< -3\end{matrix}\right.\)

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii

,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

Mình không biết sin lỗi vạn

\(a,ĐK:x\ge\dfrac{1}{5}\\ PT\Leftrightarrow5x-1=64\\ \Leftrightarrow x=13\left(tm\right)\\ b,ĐK:x\ge\dfrac{2}{5}\\ BPT\Leftrightarrow5x-2< 16\\ \Leftrightarrow x< \dfrac{18}{5}\\ \Leftrightarrow\dfrac{2}{5}\le x< \dfrac{18}{5}\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\left|x-1\right|-\left|x-2\right|=x-3\\ \Leftrightarrow\left[{}\begin{matrix}1-x-\left(2-x\right)=x-3\left(x< 1\right)\\x-1-\left(2-x\right)=x-3\left(1\le x< 2\right)\\x-1-\left(x-2\right)=x-3\left(x\ge2\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(ktm\right)\\x=0\left(tm\right)\\x=4\left(tm\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)

<=> \(\left(\sqrt{x+2}\right)^2\)> x²

<=>  \(x+2>x^2\)

<=> \(-\left(x^2-x-2\right)>0\)

<=>\(x^2-x-2< 0\)

<=> \(x^2-2x+x-2< 0\)

<=> \(\left(x-2\right)\left(x+1\right)< 0\) vì 2 tích nhân với nhau nhỏ hơn 0 nên 

<=> \(\orbr{\begin{cases}x-2>0\\x+1< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>2\\x< -1\end{cases}}\) 

và \(\orbr{\begin{cases}x-2< 0\\x+1>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 2\\x>-1\end{cases}}\)

Mình nhập 0;1 nó cho sai!!