Theo đề, ta có: \(\dfrac{-2}{2\cdot a}=\dfrac{-1}{2}\)

=>2a=4

=>a=2

Vậy: (P): 2x²+2x+c

Thay x=-1 và y=7 vào (P), ta được:

2-2+c=7

hay c=7

a: Theo đề, ta có:

\(\left\{{}\begin{matrix}a-2+c=0\\4a+c+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+c=2\\4a+c=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3a=-6\\a+c=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\c=0\end{matrix}\right.\)

(P): y = ax2 + bx + c

Parabol đi qua A(0 ; –1) ⇒ –1 = a.02 + b.0 + c ⇒ c = –1.

Parabol đi qua B(1 ; –1) ⇒ –1 = a.12 + b.1 + c ⇒ a + b + c = –1.

Mà c = –1 ⇒ a + b = 0 (1)

Parabol đi qua C(–1; 1) ⇒ a.(–1)2 + b.(–1) + c = 1 ⇒ a – b + c = 1.

Mà c = –1 ⇒ a – b = 2 (2)

Từ (1) và (2) ⇒ a = 1; b = –1.

Vậy a = 1 ; b = –1 ; c = –1.

Vì parabol đi qua ba điểm A, B, C nên ta có hệ phương trình:

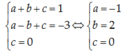
Vậy (P): y = -x² + 2x

Chọn C.

(P) : y = ax2 + bx + c

Parabol có đỉnh I(1 ; 4) ⇒ –b/2a = 1 ⇒ b = –2a ⇒ 2a + b = 0.

Parabol đi qua I(1; 4) ⇒ 4 = a.12 + b . 1 + c ⇒ a + b + c = 4.

Paraol đi qua D(3; 0) ⇒ 0 = a.32 + b.3 + c ⇒ 9a + 3b + c = 0.

Giải hệ phương trình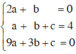  

ta được : a = –1 ; b = 2 ; c = 3.

Vậy a = –1 ; b = 2 ; c = 3.

Theo đề, ta có:

-b/2a=-2 và a+b+1=6

=>b/2a=2 và a+b=5

=>2a=2b và a+b=5

=>a=b=2,5

+ Parabol y = ax2 + bx + c đi qua điểm A (8; 0)

⇒ 0 = a.82 + b.8 + c ⇒ 64a + 8b + c = 0 (1).

+ Parabol y = ax2 + bx + c có đỉnh là I (6 ; –12) suy ra:

–b/2a = 6 ⇒ b = –12a (2).

–Δ/4a = –12 ⇒ Δ = 48a ⇒ b2 – 4ac = 48a (3) .

Thay (2) vào (1) ta có: 64a – 96a + c = 0 ⇒ c = 32a.

Thay b = –12a và c = 32a vào (3) ta được:

(–12a)2 – 4a.32a = 48a

⇒ 144a2 – 128a2 = 48a

⇒ 16a2 = 48a

⇒ a = 3 (vì a ≠ 0).

Từ a = 3 ⇒ b = –36 và c = 96.

Vậy a = 3; b = –36 và c = 96.

Lời giải:
$(P)$ cắt trục tung tại điểm có tung độ $-1$ tức $(P)$ đi qua $(0; -1)$

$\Rightarrow -1=a.0^2-2.0+c$

$\Rightarrow c=-1$

Để $P$ có min $=\frac{-4}{3}$ thì:
\(\left\{\begin{matrix} a>0\\ \frac{4ac-b^2}{4a}=\frac{-4a-(-2)^2}{4a}=\frac{-4a-4}{4a}=\frac{-(a+1)}{a}=\frac{-4}{3}\end{matrix}\right.\)  

\(\Leftrightarrow a=3\)

Vậy parabol là $y=3x^2-2x-1$

Công thức đó có ở nhiều chuyên đề về parabol rồi mà bạn.

Chứng minh như sau

Giả sử ta có parabol $y=ax^2+bx+c$

$y=a(x^2+\frac{b}{a}x)+c=a(x+\frac{b}{2a})^2+\frac{4ac-b^2}{4a}$

Nếu $a>0$ thì $y\geq \frac{4ac-b^2}{4a}$. Tức là $y_{\min}=\frac{4ac-b^2}{4a}$. Giá trị này đạt tại $x+\frac{b}{2a}=0\Leftrightarrow x=-\frac{b}{2a}$

Vậy điểm cực tiểu của đths có tọa độ $(\frac{-b}{2a}, \frac{4ac-b^2}{4a})$

Ngược lại $a< 0$ thì là cực đại và tọa độ như trên.