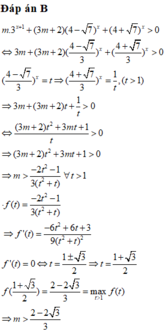Tìm m để bất phương trình x³ - x² + (m - 2)x + m 0 nghiệm đúng với mọi x > 0

Những câu hỏi liên quan
Bài 3: Tìm m để bất phương trình: x2 - 2x + 1 - m2 ≤ 0 nghiệm đúng với ∀x ∈ [1; 2]. Bài 4: Tìm m để bất phương trình: (m - 1)x2 + (2 - m)x- 1 0 có nghiệm đúng với mọi∀x ∈ (1; 2). Bài 5: Tìm m để bất phương trình: 3(m - 2)x2 + 2(m + 1)x + m - 1 0 có nghiệm đúngvới mọi ∀x ∈ (-1; 3). ...
Đọc tiếp
Bài 3: Tìm m để bất phương trình: x2 - 2x + 1 - m2 ≤ 0 nghiệm đúng với ∀x ∈ [1; 2]. Bài 4: Tìm m để bất phương trình: (m - 1)x2 + (2 - m)x- 1 > 0 có nghiệm đúng với mọi∀x ∈ (1; 2). Bài 5: Tìm m để bất phương trình: 3(m - 2)x2 + 2(m + 1)x + m - 1 < 0 có nghiệm đúngvới mọi ∀x ∈ (-1; 3). Bài 6: Tìm m để bất phương trình m2 - 2mx + 4 > 0 có nghiệm đúng với mọi ∀x ∈ (-1;0,5)
3:
x^2-2x+1-m^2<=0
=>(x-1)^2-m^2<=0
=>(x-1)^2<=m^2
=>-m<=x-1<=m
=>-m+1<=x<=m+1
mà x thuộc [-1;2]
nên -m+1>=-1 và m+1<=2
=>-m>=-2 và m<=1
=>m<=2 và m<=1
=>m<=1
Đúng 0
Bình luận (0)
Mọi người giúp mik với ạ!
Tìm m để bất phương trình x³ - x² + (m - 2)x + m 0 nghiệm đúng với mọi x > 0
Giúp mình 2 câu này với ạ:
1. Tìm m để bất phương trình sau có nghiệm đúng với mọi x :
mx2 +(m+1)x+m-1 <0
2. Tìm m để bất phương trình sau vô nghiệm :
mx2-4(m+1)x+m-5<0
1.
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta=\left(m+1\right)^2-4m\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\-3m^2+7m+1< 0\end{matrix}\right.\)
\(\Leftrightarrow m< \dfrac{7-\sqrt{61}}{6}\)
2.
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\Delta'=4\left(m+1\right)^2-m\left(m-5\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\3m^2+13m+4\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\-4\le m\le-\dfrac{1}{3}\end{matrix}\right.\)
Không tồn tại m thỏa mãn
Đúng 4
Bình luận (3)
Cho hàm số F(x) = (m + 1)x2 - 2mx + m - 2 (m là tham số). a) Tìm m để phương trình f(x) = 0 có hai nghiệm trái dấu? b) Tìm m để bất phương trình f(x) < 0 có một nghiệm đúng với mọi x.
Với thì PT có nghiệm (chọn)
Với thì là đa thức bậc 2 ẩn
có nghiệm khi mà
Tóm lại để có nghiệm thì
tìm giá trị m để bất phương trình sau có nghiệm đúng với mọi x. (m-2)x^2+2mx-2-m<0
Để phương trình có nghiệm đúng với mọi x thì
(2m)^2-4(m-2)(-m-2)<0 và m-2<0
=>4m^2+4(m^2-4)<0 và m<2
=>8m^2-16<0 và m<2
=>m^2<2
=>-căn 2<m<căn 2
Đúng 0
Bình luận (0)
Cho bất phương trình
m
.
3
x
+
1
+
(
3
m
+
2
)
(
4
-
7
)
x
+
(
4
+
7
)...
Đọc tiếp
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0
với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x ∈ ( - ∞ , 0 )
A. m > 2 + 2 3 3
B. m > 2 - 2 3 3
C. m ≥ 2 - 2 3 3
D. m ≥ - 2 - 2 3 3
Tìm tất cả các giá trị của tham số m để bất phương trình( m - 1) x^2-2x + m + 1> 0 nghiệm đúng với mọi x> 0
Cho bất phương trình
m
.
3
x
+
1
+
(
3
m
+
2
)
(
4
-
7
)...
Đọc tiếp
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0 với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho có nghiệm đúng với mọi x ∈ - ∞ ; 0
A. m ≥ 2 - 2 3 3
B. m > 2 - 2 3 3
C. m > 2 + 2 3 3
D. m ≥ - 2 - 2 3 3
Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt  , tìm điều kiện của t.
, tìm điều kiện của t.
Đưa về bất phương trình dạng ![]()
Cách giải :
![]()

Ta có 

Đặt  , khi đó phương trình trở thành
, khi đó phương trình trở thành
![]()

![]()
![]()
![]()
![]()
Ta có: 



Vậy 
Đúng 0
Bình luận (0)
tìm giá trị của m để bất phương trình (m+1)x2-2(m+1)x+4<0 nghiệm đúng với mọi giá trị của x
- Với \(m=-1\Rightarrow4< 0\) không thỏa mãn
- Với \(m\ne-1\) BPT nghiệm đúng với mọi x khi và chỉ khi:
\(\left\{{}\begin{matrix}m+1< 0\\\Delta'=\left(m+1\right)^2-4\left(m+1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -1\\\left(m+1\right)\left(m-3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -1\\-1< m< 3\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn yêu cầu
Đúng 0
Bình luận (0)