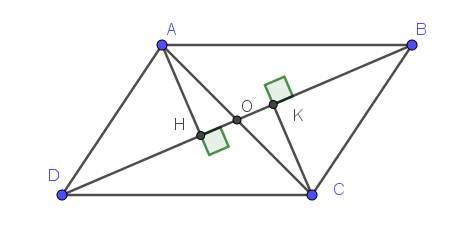
Cho hình bình hành ABCD,O là giao điểm của hai đường chéo. AH vuông góc BD .Biết các góc DAH;HAO;OAB bằng nhau.CMR ABCD là hình chữ nhật.

Những câu hỏi liên quan
Cho hình bình hành ABCD , O là giao điểm của hai đường chéo, H là hình chiếu của A trên OD . Biết rằng các góc DAH ; HAO ; OAB bằng nhau . Chứng minh ABCD là hình chữ nhật.
Cho hình bình hành ABCD O là giao điểm của 2 đường chéo. Vẽ AH và CK vuông góc với BD. a) cm tứ giác AHCK là hình bình hành.
Lời giải:
Vì $ABCD$ là hình bình hành nên $AO=OC$
Xét tam giác $AHO$ và $CKO$ có:
$\widehat{AHO}=\widehat{CKO}=90^0$
$\widehat{AOH}=\widehat{COK}$ (đối đỉnh)
$AO=CO$
$\Rightarrow \triangle AHO=\triangle CKO$ (ch-gn)
$\Rightarrow AH=CK$
Tứ giác $AHCK$ có 2 cạnh đối $AH, CK$ song song (do cùng vg với $BD$) và bằng nhau nên $AHCK$ là hbh.
Đúng 1
Bình luận (0)
Ai giúp mình làm mấy câu này với
1: Cho hình bình hành ABCD, gọi O là giao điểm của hai đường chéo, H là hình chiếu của A trên OD. Biết rằng các góc DAH, HAO,OAD bằng nhau. CMR: ABCD là Hình chữ nhật
2: Cho tam giác ABC vuông tại A, đường cao AH. Gọi I và K theo thứ tự là hình chiếu của H trên AD và AC, gọi M là trung điểm của BC. CMR: AM vuông góc với IK
câu 1
gọi góc DAH = góc HAO =góc OAB = x
Xét tam giác OAD cân tại A(....)
=> góc ADH = 90 độ - x (1)
=> góc DOC = 180 độ - 2x (góc ngoài)
_góc ACD=x ( soletrong ...)
Xét tam giác ODC có
góc ODC = 180 độ - góc ACD - góc DOC
=180 độ - 180 độ + 2x -x
= x
=> góc ODC = x (2)
từ (1) và (2) => góc ADC = 90 độ - x + x =90 độ
=> H.B.Hành có 1 góc vg^ => đó là H.C.Nhật (dpcm)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD, 2 đường chéo cắt nhau tại O. Kẻ AH vuông góc BD, CD vuông góc BD (AC ko vuông góc BD)
a) C/m tứ giác AHCK là hình bình hành
b)Biết AH cắt CD tại M, CK cắt AB tại N. C/m O là trung điểm của MN
a) Xét hai tam giác vuông ADH và BCK có:
AD = BC (tính chất hình bình hành)
B1ˆ=D2ˆB1^=D2^ (slt, AB // CD)
Vậy: ΔADH=ΔBCK(ch−gn)ΔADH=ΔBCK(ch−gn)
⇒⇒ AH = CK (1)
Chứng minh tương tự ta được: ΔABK=ΔCDH(ch−gn)ΔABK=ΔCDH(ch−gn)
⇒⇒ AK = CH (2)
Từ (1) và (2) suy ra: AHCK là hình bình hành
b) O là giao điểm của AC và BD thì O là trung điểm của AC (tính chất đường chéo hình bình hành)
AHCK là hình bình hành (cmt) ⇒⇒ HK đi qua trung điểm O của đường chéo AC
Vậy H, O, K thẳng hàng.
P.s:Mìh vẽ hình hơi xấu ;))
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là hình chiếu của H trên AB, AC. Gọi M là trung điểm của BC. Chứng minh rằng AM vuông góc với IK.Bài 2: Cho hình bình hành ABCD, O là giao điểm hai đường chéo, H là hình chiếu của A trên OD. Biết rằng các góc DAH, HAO, OAB bằng nhau. Chứng minh rằng ABCD là hình chữ nhật.
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là hình chiếu của H trên AB, AC. Gọi M là trung điểm của BC. Chứng minh rằng AM vuông góc với IK.
Bài 2: Cho hình bình hành ABCD, O là giao điểm hai đường chéo, H là hình chiếu của A trên OD. Biết rằng các góc DAH, HAO, OAB bằng nhau. Chứng minh rằng ABCD là hình chữ nhật.
Cho hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Giải thích các khẳng định sau:
a) Nếu \(\widehat {{\rm{BAD}}}\) là góc vuông thì \(\widehat {{\rm{ADC}}}\) và \(\widehat {{\rm{ABC}}}\) cũng là góc vuông.
b) Nếu \(AC = BD\) thì \(\widehat {{\rm{BAD}}}\) vuông.

a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\), \(BD\)
\(AB = CD\); \(AD = BC\); \(AB\) // \(CD\); \(AD\) // \(BC\)
Nếu \(\widehat {{\rm{BAD}}} = 90^\circ \) suy ra \(AB \bot AD\)
Mà \(AB\) // \(CD\); \(AD\) // \(BC\)
Suy ra \(AD \bot CD;\;AB \bot BC\)
Suy ra \(\widehat {ADC} = \widehat {ABC} = 90^\circ \)
b) Xét \(\Delta BAD\) và \(\Delta CDA\) ta có:
\(BA = CD\) (gt)
\(AD\) chung
\(BD = AC\) (gt)
Suy ra \(\Delta BAD = \Delta CDA\) (c-c-c)
Suy ra \(\widehat {{\rm{BAD}}} = \widehat {{\rm{CDA}}}\) (hai góc tương ứng)
Mà \(\widehat {BAD} + \widehat {CDA} = 180^\circ \)(do \(AB\) // \(CD\) , cặp góc trong cùng phía)
Suy ra \(\widehat {BAD} = \widehat {CDA} = 90^\circ \)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có O là giao điểm hai đường chéo, kẽ AH và CK vuông góc với DB lần lượt tại H và K. Chứng minh:
a/ AHCK là hình bình hành.
b/ H đối xứng với K qua O.
Cho hình bình hành ABCD. Hai đường chéo cắt nhau tại O. Kẻ AK vuông góc BC, AH vuông góc CD, biết góc HDK=140độ. Tính các góc của hình bình hành.
Anh chị giúp em nha !!!
Cho hình bình hành ABCD, đường chéo BD. Kẻ AH và CK vuông góc với BD ở H và ở K.
a) chứng minh tứ giác AHCK là hình bình hành
b) gọi O là trung điểm của HK
c/m 3 điểm A,O,C thẳng hàng
a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
góc ADH=góc CBK
=>ΔAHD=ΔCKB
=>AH=CK
mà AH//CK
nên AHCK là hình bình hành
b: AHCK là hbh
=>AC cắt HK tại trung điểm của mỗi đường
=>A,O,C thẳng hàng
Đúng 1
Bình luận (0)