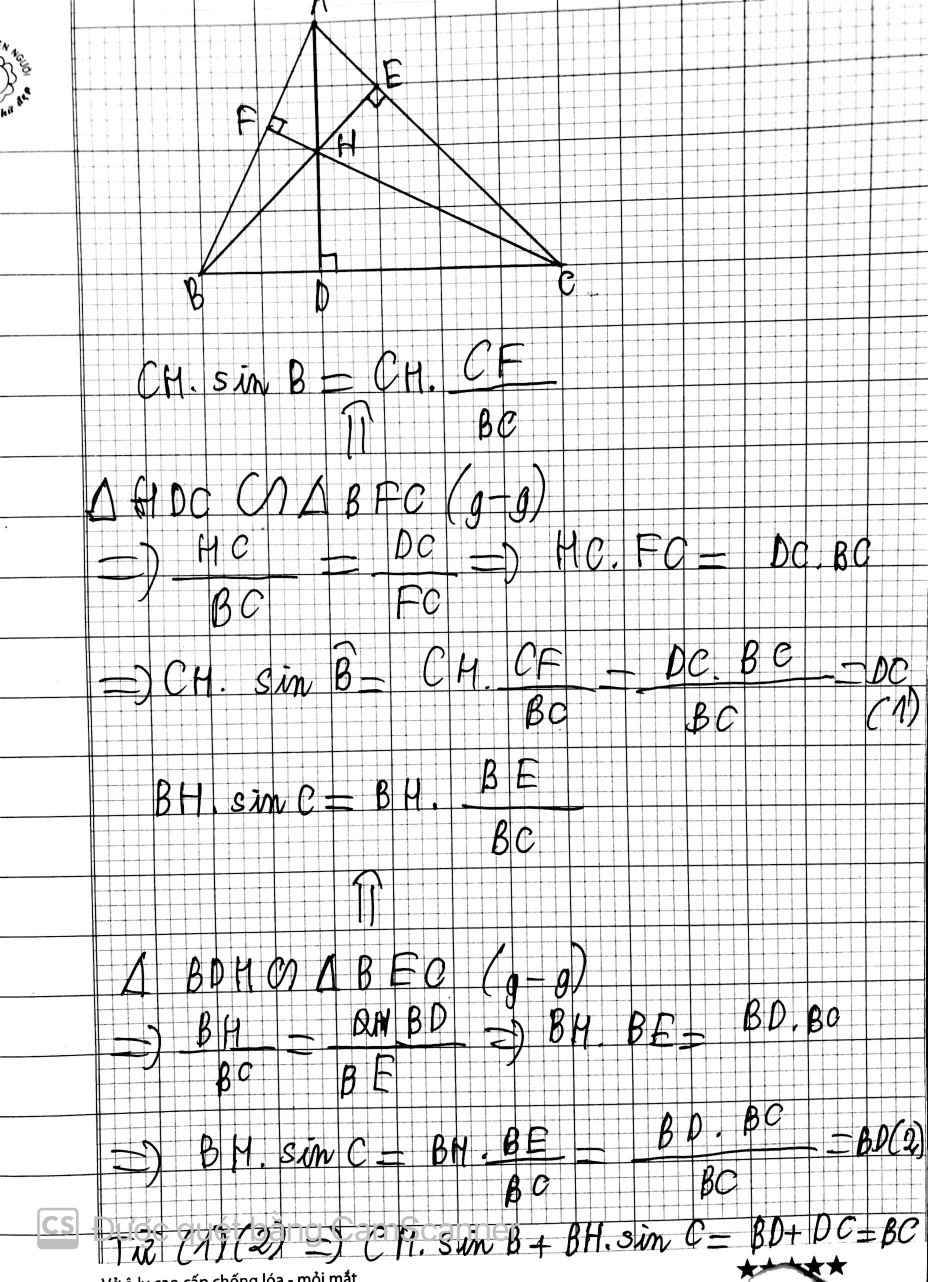Giúp tớ với: Cho tam giác ABC, H là trực tâm. C/m CH.sinB+BH.sinC=bc

Những câu hỏi liên quan
Cho tam giác ABC, H là trực tâm. C/m CH.sinB+BH.sinC=bc
Cho tam giác ABC, H là trực tâm. C/m CH.sinB+BH.sinC=bc
Cho \(\Delta ABC\), H là trực tâm. Chứng minh \(CH.sinB+BH.sinC=BC\)
Cảm ơn trước ★
cho tam giác ABC nhọn trực tâm H nội tp đg tròn (O) Gọi H' là điểm đối xứng của H qua BC CM
a, tg ABH'C là tg nội tiêp
b.bán kính đg tròn ngoại tiếp tam giác BHC = bk đg tròn ngoạn tp tam giác ABC
giúp tớ với tớ đang cần gấp
Cho tam giác ABC có A>90. H là trực tâm. O là giao điểm 3 đường trung trực. Vẽ D sao cho O là trung điểm AD
a) C/m: BH//CD; BH=CD
b) Kẻ OM vuông góc với BC. C/m: M là trung điểm HD
c) Gọi G là trọng tâm tam giác ABC. C/m: H,G,O thẳng hàng
a) Chứng minh BH//CD và BH=CD:
Vì O là giao điểm 3 đường trung trực nên O là tâm đường tròn ngoại tiếp tam giác ABC.
Vì A>90 nên tâm đường tròn ngoại tiếp tam giác ABC nằm ngoài tam giác ABC.
Vì H là trực tâm nên AH ⊥ BC và AH cắt BC tại D.
Vì O là trung điểm AD nên OD = AO.
Vì O là tâm đường tròn ngoại tiếp tam giác ABC nên OB = OC.
Từ đó suy ra OB = OC = OD = AO.
Vậy tứ giác OBCD là tứ giác nội tiếp.
Do đó, ta có: (BHCD) => ∠BHC + ∠BDC = 180°
Mà ∠BHC + ∠BDC = 90° + 90° = 180°
Vậy BH // CD và BH = CD.
b) Chứng minh M là trung điểm HD:
Vì OM ⊥ BC và H là trực tâm nên HM // BC.
Vì HM // BC và BH // CD nên HM // CD.
Do đó, ta có: (HMD) => ∠HMD + ∠HCD = 180°
Mà ∠HMD + ∠HCD = 90° + 90° = 180°
Vậy HM // CD và HM = CD/2.
Do đó, M là trung điểm HD.
c) Chứng minh H, G, O thẳng hàng:
Gọi E, F lần lượt là trung điểm của AB, AC.
Ta có: EG // HO và EG = (2/3)HO
Do đó, ta có: H, G, O thẳng hàng.
Đúng 1
Bình luận (2)
Cho tam giác ABC có góc A= 60 độ, trực tâm H . Gọi M là điểm đối xứng với H qua BC
a, C/M tam giác BHC = tam giác BMC
b, Tính BMC
a) Vì M đối xứng với H qua BC nên BC là đường trung trực của MH
Suy ra: BH=BM và CH=CM
Xét ΔBHC và ΔBMC có
BH=BM(cmt)
CH=CM(cmt)
BC chung
Do đó: ΔBHC=ΔBMC(c-c-c)
Đúng 0
Bình luận (0)
Cho tam giác ABC trực tâm H,M là trung điểm của BC,gọi O là giao 3 trung trực tam giác ABC,G là trọng tâm tam giác ABC.Chứng minh a) 2OM=AH và b) chứng minh H,G,O thẳng hàng
Mn giúp e với e thật sự cần gấp tks mn
Cho tam giác ABC có trực tâm là H. M và N lần lượt là trung điểm của BC và AC. Đường trung trực BC cắt đường trung trực AC tại O.
a) Chứng minh tam giác AHB đồng dạng với tam giác MON
b) Gọi G là trực tâm tam giác ABC. Chứng minh G, H, O thẳng hàng.
a: OM//AH
ON//BH
MN//AB
=>góc BAH=góc OMN và góc ABH=góc ONM
=>ΔABH đồng dạng vơi ΔMNO
b: G là trọng tâm của ΔABC
=>GM/GA=1/2
ΔABH đồng dạng với ΔMNO nên OM/AH=MN/AB=1/2
=>OM/AH=MG/AG
=>ΔHAG đồng dạng với ΔOMG
c: ΔHAG đồng dạng với ΔOMG
=>góc AGH=góc OGM
=>H,G,O thẳng hàng
Đúng 0
Bình luận (0)
cho tam giác abc có M trung điểm của BC ,N là trung điểm của AC ,đường trung trực BC cắt dường trung trực của AC tại O,gọi H là trực tâm tam giác ABC
a cm tam giác AHB đồng dạng tam giác MNO
b gọi G là giao điểm của OH với AM cmr G là trọng tâm của tam giác ABC
a: OM//AH
ON//BH
MN//AB
=>góc BAH=góc OMN và góc ABH=góc ONM
=>ΔABH đồng dạng với ΔMNO
b: A,G,M thẳng hàng và H,G,O thẳng hàng
=>góc AGH=góc MGO
=>ΔAHG đồng dạng với ΔMOG
=>OM/AH=MG/AG
=>OM/AH=MN/AB=1/2
=>GM/GA=1/2
=>G là trọng tâm của ΔACB
Đúng 0
Bình luận (0)