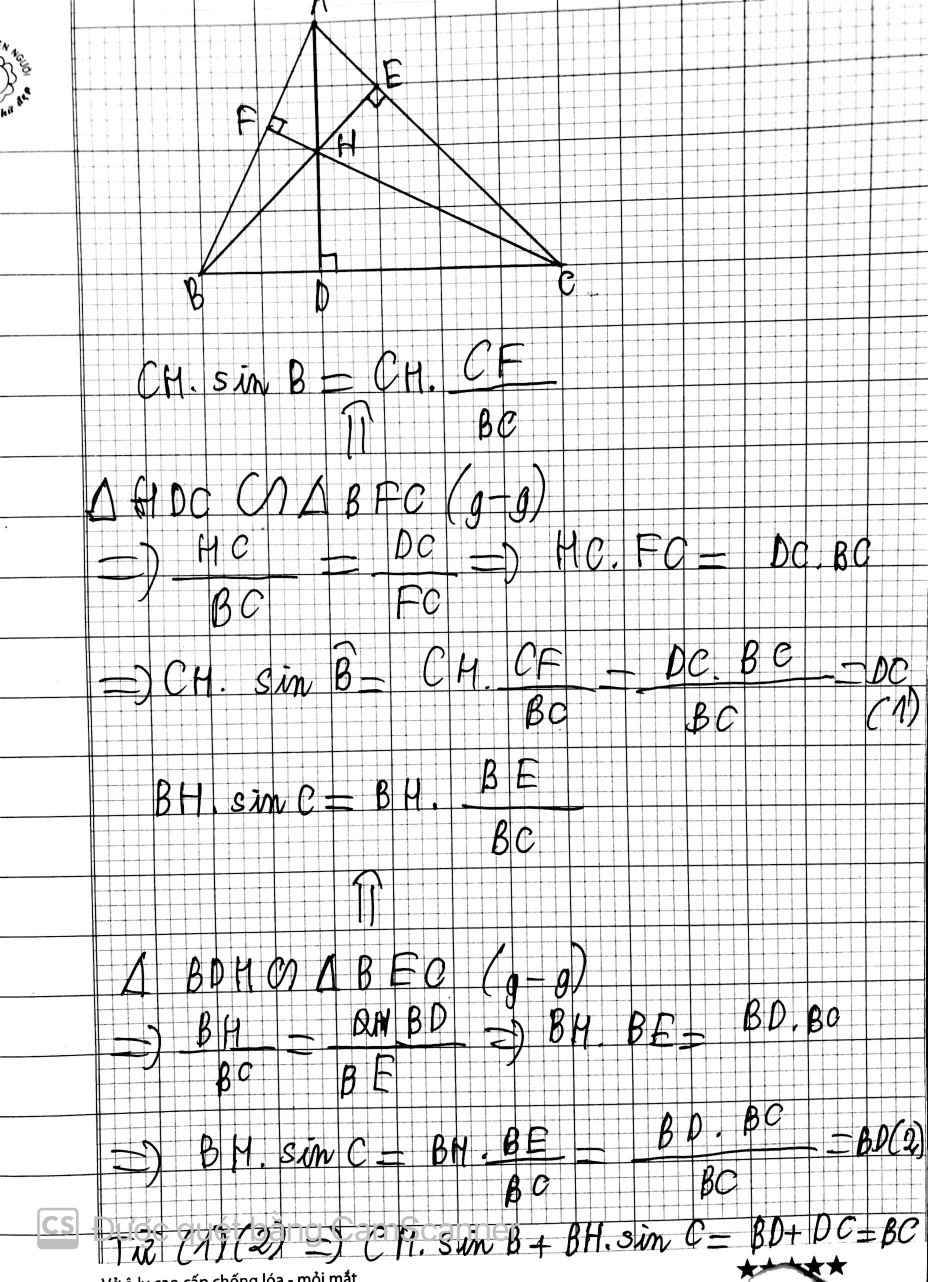Ôn tập Hệ thức lượng trong tam giác vuông
Các câu hỏi tương tự
cho ΔABC có góc A 105°,góc B60°,ABa. lấy điểm E trên BC sao cho BEa. Kẻ ED song song với AB(D thuộc AD). AH là hình chiếu của A trên BC(H thuộc BC). Đường thẳng qua A vuông góc với AC cắt BC tại F
a)chứng minh tam giác ABE đều và tính AH theo a
b)chứng minh
góc EADgóc EAF45°. từ đó chứng minh ΔAEFΔAED
c)chứng minh: 1/AD2+1/AC23/4a2
cảm ơn rất nhiều
Đọc tiếp
cho ΔABC có góc A =105°,góc B=60°,AB=a. lấy điểm E trên BC sao cho BE=a. Kẻ ED song song với AB(D thuộc AD). AH là hình chiếu của A trên BC(H thuộc BC). Đường thẳng qua A vuông góc với AC cắt BC tại F
a)chứng minh tam giác ABE đều và tính AH theo a
b)chứng minh
góc EAD=góc EAF=45°. từ đó chứng minh ΔAEF=ΔAED
c)chứng minh: 1/AD2+1/AC2=3/4a2
cảm ơn rất nhiều
Cho Tam giác ABC nhọn đường cao AD (à thuộc BC. Gọi H là điểm thuộc đoạn AD sao cho DA.DH=DB.DC BH cắt CA tại E, CH cắt AB tại F. Chứng minh rằng: 1. Hai tam giác DAB, DCH đồng dạng và H là trực tâm của Tam giác ABC 2. AE.AC=AH.AD=AF.AB 3. AH.AD+BH.BE+CH.CF=AB^2+BC^2+AC^2/2 Giúp mình câu 3 với ạ mình cảm ơn
Cho ΔABC vuông tại A, đường cao AH, biết BH = 1,6cm, CH=2,5cm. Kẻ HE⊥AB (E ϵ AB), HF⊥AC (F ϵ AC)
a) Chứng minh ΔAFE ~ ΔABC, Tính diện tích ΔAEF
b) Đường thẳng đi qua A vuông góc với EF tại K cắt BC ở I. Chứng minh I là trung điểm của BC
(Các bạn giúp mình với ạ, mình cảm ơn ^^)
Cho tam giác ABC vuông tại A (AB > AC), có đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường tròn (C) tại điểm thứ hai D
a) chứng minh BC là đường trung trực của AD
b) Chứng minh BD là tiếp tuyến của đường tròn (C).
cho \(\Delta ABC\) nhọn,đường cao AH. Gọi M,N lần lượt là hình chiếu của H trên AB,AC.
a) Chứng minh AM.AB=AN.AC
b) chứng minh \(AH=\dfrac{BC}{cotB+cotC}\)
c) cho \(BC=MN\sqrt{2}\). Chứng minh \(S_{\Delta AMN}=S_{\Delta BMNC}\)
Cho DeltaABC vuông tại A có AB 5 và AC 4
a) Giải DeltaABC .
b) Kẻ đường cao AH của DeltaABC . chứng minh : BC là tiếp tuyến của ( A ; AH ).
c) từ H kẻ HE perpAC cắt ( A ) tại K . Chứng minh BI là tiếp tuyến của (A).
Chứng minh : BI là tiếp tuyến của (A).
d) Chứng minh : 3 điểm I , A , K thẳng hàng .
Đọc tiếp
Cho \(\Delta\)ABC vuông tại A có AB = 5 và AC = 4
a) Giải \(\Delta\)ABC .
b) Kẻ đường cao AH của \(\Delta\)ABC . chứng minh : BC là tiếp tuyến của ( A ; AH ).
c) từ H kẻ HE \(\perp\)AC cắt ( A ) tại K . Chứng minh BI là tiếp tuyến của (A).
Chứng minh : BI là tiếp tuyến của (A).
d) Chứng minh : 3 điểm I , A , K thẳng hàng .
Cho tam giác ABC, H là trực tâm. Chứng minh rằng: CH×sinB+BH×sinC= BC
Giải giúp mình nhé, cảm ơn nhiều:
Cho \(\Delta\)ABC nhọn có 3 đường cao là AD, BE, CF cắt nhau tại H.
a. Chứng minh AH.HD = BH.HE = CH.HF
b. Chứng minh AD là tia phân giác của góc EDF
c. Chứng minh \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=1\)
Cho ΔABC, đường cao AH (H nằm giữa B và C). AH = 12cm, HB=9cm, BC = 25cm.
a) CM: ΔABC vuông tại A.
b) Kẻ Bx// AC cắt AH ở D.Tính HD và chứng minh: AB2 = AC.BD.
c) Kẻ DE⊥AC (E ϵ AC), DE cắt BC ở F. CM: BH2 = HF.HC