Cho ABC vuông tại A có 0 ABC 60 = . Trên cạnh BC, lấy điểm M sao BM = BA. a) Chứng minh : ABM đều và MAC cân.

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có ABC = 60°.a) Tính số đo góc BCA.b) Tia phân giác của góc ABC cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BE = BA. Chứng minh tam giác ADB = tam giác EDB và DE vuông góc với BC.c) Trên tia BA lấy điểm M sao cho BM = BC. Chứng minh Ba điểm E, D, M thẳng hàng .
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ACB}=90^0-\widehat{ABC}\)
\(\Leftrightarrow\widehat{ACB}=90^0-60^0\)
hay \(\widehat{ACB}=30^0\)
Vậy: \(\widehat{ACB}=30^0\)
b) Xét ΔADB và ΔEDB có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔADB=ΔEDB(c-g-c)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
hay DE\(\perp\)BC(đpcm)
c) Ta có: BE+EC=BC(E nằm giữa B và C)
BA+AM=BM(A nằm giữa B và M)
mà BE=BA(ΔBED=ΔBAD)
và BC=BM(gt)
nên EC=AM
Xét ΔADM vuông tại A và ΔEDC vuông tại E có
DA=DE(ΔDAB=ΔDEB)
AM=EC(cmt)
Do đó: ΔADM=ΔEDC(hai cạnh góc vuông)
nên \(\widehat{ADM}=\widehat{EDC}\)(hai góc tương ứng)
mà \(\widehat{EDC}+\widehat{ADE}=180^0\)(hai góc kề bù)
nên \(\widehat{ADM}+\widehat{ADE}=180^0\)
\(\Leftrightarrow\widehat{EDM}=180^0\)
hay E,D,M thẳng hàng(đpcm)
Đúng 3
Bình luận (0)
Cho ∆ABC vuông tại A, có BM là phân giác của ABC ̂. Trên cạnh BC lấy điểm H sao
cho BH = BA.
a) Chứng minh ∆ABM = ∆HBM, từ đó suy ra MH vuông góc với BC
b) Chứng minh ∆MAH cân
c) Kéo dài tia HM cắt tia BA tại F. Chứng minh ∆MAF = ∆MHC
Bài 4: Cho biết ∆ABC ∆MNK, trong đó có BC 15cm, 0 0 45 ˆ 60 , Bˆ C . Tính độ dài cạnh NK và số đo Mˆ của ∆MNK.Bài 5: Cho ∆ABC vuông tại A có AB AC. Trên cạnh BC lấy điểm D sao cho BD BA. Gọi M là trung điểm của cạnh AD.1) Chứng minh ∆ABM ∆DBM. 2) Vẽ tia BM cắt cạnh AC tại E. Chứng minh ED ⊥ BD. 3) Chứng minh ∆AME ∆DME. 4) Trên cạnh MD lấy điểm I sao cho MI ID. Qua I vẽ đường thẳng vuông góc với cạnh MD cắt cạnh ED tại K. Từ M vẽ đường thẳng vuông góc với cạnh AB tại H. Chứng minh ba điể...
Đọc tiếp
Bài 4: Cho biết ∆ABC =∆MNK, trong đó có BC = 15cm, 0 0 45 ˆ 60 , Bˆ = C = . Tính độ dài cạnh NK và số đo Mˆ của ∆MNK.
Bài 5: Cho ∆ABC vuông tại A có AB < AC. Trên cạnh BC lấy điểm D sao cho BD = BA. Gọi M là trung điểm của cạnh AD.
1) Chứng minh ∆ABM = ∆DBM.
2) Vẽ tia BM cắt cạnh AC tại E. Chứng minh ED ⊥ BD.
3) Chứng minh ∆AME = ∆DME.
4) Trên cạnh MD lấy điểm I sao cho MI = ID. Qua I vẽ đường thẳng vuông góc với cạnh MD cắt cạnh ED tại K. Từ M vẽ đường thẳng vuông góc với cạnh AB tại H. Chứng minh ba điểm H, M, K thẳng hàng.
Hmm....................................................![]()
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A có góc C=30°. Trên cạnh BC lấy 2 điểm M và N sao cho BM=BA
a, Tính số đo góc B cm tam giác AMB đều
b, Tính góc MAC. Tam giác AMC là tam giác gì vì sao
c, chứng minh AM=1/2
Cho tam giác ABC vuông tại A Trên tia BC , lấy điểm M sao cho BM = BA . Chứng minh :
A,Chưng minh Tam giác ABM đều
B,AB = BC/2
Cho tam giác ABC có BA<BC và góc B=60 độ
a) Trên BC lấy điểm M sao cho BM=BA.Chứng minh tam giác ABM đều
b) Tia phân giác góc B cắt Ac tại D. Chứng minh tam BAD=BMD
c) Tia MD cắt tia BA tại H, chứng minh tam giác DHC cân
Cho tam giác ABC có BA<BC và góc B=60 độ
a) Trên BC lấy điểm M sao cho BM=BA.Chứng minh tam giác ABM đều
b) Tia phân giác góc B cắt Ac tại D. Chứng minh tam BAD=BMD
c) Tia MD cắt tia BA tại H, chứng minh tam giác DHC cân
Ta có BA=BM (gt)
^B=60 độ
=>ΔABM là Δ đều
Đúng 1
Bình luận (0)
xét ΔBAD và ΔBMD
có AB=BM
^ABD=^MBD
BD chnsg
suy ra ΔBAD =ΔBMD
Đúng 1
Bình luận (0)
Bài 5: Cho tam giác ABC cân tại A. Trên cạnh AC lấy điểm M, trên cạnh AB lấy điểm N sao cho AM = AN.
a) Chứng minh ABM=ACN
b) Gọi I là giao điểm của BM và CN. Chứng minh △ IBC cân.
Cho tam giác ABC vuông tại A,
A
C
B
^
30
°
. Tia phân giác của góc ABC cắt cạnh AC tại M. Lấy điểm K trên cạnh BC sao cho BK BA.a) Chứng minh
∆
A
B
M
∆
K
B
M
b) Gọi E là giao điểm của các đường thẳng AB và KM. Chứng minh tam giác MEC cân.c) Chứng minh tam giác BEC đều.d) Kẻ
A
H
⊥
E...
Đọc tiếp
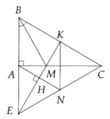
Cho tam giác ABC vuông tại A, A C B ^ = 30 ° . Tia phân giác của góc ABC cắt cạnh AC tại M. Lấy điểm K trên cạnh BC sao cho BK = BA.
a) Chứng minh ∆ A B M = ∆ K B M
b) Gọi E là giao điểm của các đường thẳng AB và KM. Chứng minh tam giác MEC cân.
c) Chứng minh tam giác BEC đều.
d) Kẻ A H ⊥ E M . ( H ∈ E M ) . Các đường thẳng AH và EC cắt nhau tại N. Chứng minh K N ⊥ A C .