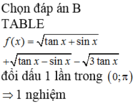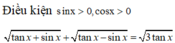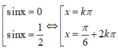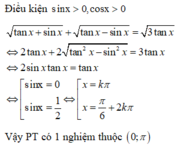cho tanx bang -2 , π/2 <x<π . tinh gia tri cosx sinx

Những câu hỏi liên quan
Tìm GTLN GTNN
y = 2cos22x + 2cos2x - 4
y = tan2x - 2√3 tanx -1 ∀ x ∈ [ -π/4 ; π/3 ]
a.
Đặt \(cos2x=t\Rightarrow t\in\left[-1;1\right]\)
Xét hàm \(y=f\left(t\right)=2t^2+2t-4\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=-\dfrac{1}{2}\in\left[-1;1\right]\)
\(f\left(-1\right)=-4\) ; \(f\left(-\dfrac{1}{2}\right)=-\dfrac{9}{2}\) ; \(f\left(1\right)=0\)
\(\Rightarrow y_{min}=-\dfrac{9}{2}\) khi \(t=-\dfrac{1}{2}\) hay \(cos2x=-\dfrac{1}{2}\)
\(y_{max}=0\) khi \(cos2x=1\)
b. Đặt \(tanx=t\Rightarrow t\in\left[-1;\sqrt{3}\right]\)
Xét hàm \(f\left(t\right)=t^2-2\sqrt{3}t-1\) trên \(\left[-1;\sqrt{3}\right]\)
\(-\dfrac{b}{2a}=\sqrt{3}\in\left[-1;\sqrt{3}\right]\)
\(f\left(-1\right)=2\sqrt{3}\) ; \(f\left(\sqrt{3}\right)=-4\)
\(y_{min}=-4\) khi \(x=\dfrac{\pi}{3}\) ; \(y_{max}=2\sqrt{3}\) khi \(x=-\dfrac{\pi}{4}\)
Đúng 1
Bình luận (0)
Chứng minh các bất đẳng thức sau: tanx > sinx, 0 < x < π /2
Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π /2);

x ∈ [0;1/2)
Dấu “=” xảy ra khi x = 0.
Suy ra f(x) đồng biến trên nửa khoảng [0; π /2)
Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)
Đúng 0
Bình luận (0)
Chứng minh các bất đẳng thức sau:
a) tanx > sinx, 0 < x < π/2
b) 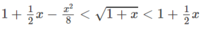
với 0 < x < + ∞
a) Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π/2);

x ∈ [0;1/2)
Dấu “=” xảy ra khi x = 0.
Suy ra f(x) đồng biến trên nửa khoảng [0; π/2)
Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)
b) Xét hàm số h(x) trên [0; + ∞ )
![]()
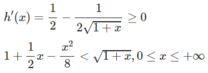
Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng [0; + ∞ ).
Vì h(x) = 0 nên
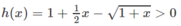
Hay
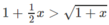
Xét hàm số trên f(x) trên [0; + ∞ );
![]()
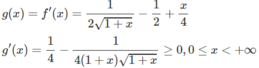
Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng [0; + ∞ ) nên g(x) ≥ 0, tức là f′(x) ≥ 0 trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng .
Mặt khác, ta có f(0) = 0 nên
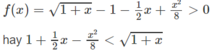
Với mọi 0 < x < + ∞ .
Đúng 0
Bình luận (0)
Nếu \(cot1,25.tan\left(4\text{ }Π+1,25\right)-sin\left(x+\frac{Π}{2}\right).cos\left(6Π-x\right)=0\) thì tanx bằng
\(cot1,25.tan\left(4\pi+1,25\right)-sin\left(x+\frac{\pi}{2}\right).cos\left(6\pi-x\right)=0\)
\(\Leftrightarrow cot1,25.tan1,25-cosx.cos\left(-x\right)=0\)
\(\Leftrightarrow1-cos^2x=0\)
\(\Leftrightarrow sin^2x=0\Rightarrow sinx=0\Rightarrow tanx=0\)
Đúng 0
Bình luận (0)
Giảt pt 1,sin(4x-10°) = √2/2 2, cos(2x=7/8 3, tan 2x=tanx 4, cot(x+π/5)=-1 5, cos3x=sin5x
1.
\(sin\left(4x-10^0\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(4x-10^0\right)=sin45^0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-10^0=45^0+k360^0\\4x-10^0=135^0+k360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=55^0+k360^0\\4x=145^0+k360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=13,75^0+k90^0\\x=36,25^0+k90^0\end{matrix}\right.\) (\(k\in Z\))
Đúng 0
Bình luận (0)
2.
Đề không đúng
3.
ĐKXĐ: \(\left\{{}\begin{matrix}cos2x\ne0\\cosx\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(tan2x=tanx\)
\(\Rightarrow2x=x+k\pi\)
\(\Rightarrow x=k\pi\)
4.
\(cot\left(x+\dfrac{\pi}{5}\right)=-1\)
\(\Leftrightarrow x+\dfrac{\pi}{5}=-\dfrac{\pi}{4}+k\pi\)
\(\Leftrightarrow x=-\dfrac{9\pi}{20}+k\pi\) (\(k\in Z\))
Đúng 0
Bình luận (0)
5.
\(cos3x=sin5x\)
\(\Leftrightarrow sin5x=sin\left(\dfrac{\pi}{2}-3x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=\dfrac{\pi}{2}-3x+k2\pi\\5x=\dfrac{\pi}{2}+3x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}8x=\dfrac{\pi}{2}+k2\pi\\2x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{16}+\dfrac{k\pi}{4}\\x=\dfrac{\pi}{4}+k\pi\end{matrix}\right.\) (\(k\in Z\))
Đúng 0
Bình luận (0)
Số nghiệm thuộc khoảng
0
;
π
của phương trình
tan
x
+
sin
x
+
tan
x
−
sin
x
3
tan
x
là. A. 0 B. 1. C. 2 D. 3
Đọc tiếp
Số nghiệm thuộc khoảng 0 ; π của phương trình tan x + sin x + tan x − sin x = 3 tan x là.
A. 0
B. 1.
C. 2
D. 3
Đáp án B
TABLE f ( x ) = tan x + sin x + tan x − sin x − 3 tan x đổi dấu 1 lần trong 0 ; π ⇒ 1 nghiệm
Đúng 0
Bình luận (0)
Số nghiệm thuộc khoảng
0
;
π
của phương trình
tan
x
+
sin
x
+
tan
x
-
sin
x
3
tan
x
là A. 0. B. 1. C. 2. D. 3.
Đọc tiếp
Số nghiệm thuộc khoảng 0 ; π của phương trình tan x + sin x + tan x - sin x = 3 tan x là
A. 0.
B. 1.
C. 2.
D. 3.
Số nghiệm thuộc khoảng
0
;
π
của phương trình.
tan
x
+
sin
x
tan
x
-
sin
x
3
tan
x
là A. 0. B. 1 C. 2. D. 3.
Đọc tiếp
Số nghiệm thuộc khoảng 0 ; π của phương trình. tan x + sin x = tan x - sin x = 3 tan x là
A. 0.
B. 1
C. 2.
D. 3.
Số nghiệm thuộc khoảng
0
;
π
của phương trình.
tan
x
+
sin
x
+
tan
x
-
sin
x
3
tan
x
là A. 0. B. 1 C. 2. D. 3
Đọc tiếp
Số nghiệm thuộc khoảng 0 ; π của phương trình.
tan x + sin x + tan x - sin x = 3 tan x là
A. 0.
B. 1
C. 2.
D. 3