Chứng minh rằng tổng sau là số chính phương:
1 mũ 3 + 2 mũ 3 +3 mũ 3 + 4 mũ 3 + 5 mũ 3
Số chính phương là số bằng bình phương của một số tự nhiên ( ví dụ: 0, 1, 4, 9, 16......). Mỗi tổng sau có là một số chính phương không?
a) 1 mũ 3 + 2 mũ 3
b) 1 mũ 3 + 2 mũ 3 + 3 mũ 3
c) 1 mũ 3 + 2 mũ 3 + 3 mũ 3 + 4 mũ 3
số chính phương là số bằng bình phương của một số tự nhiên ( ví dụ : 0, 1, 4, 9, 16,...) mỗi tổng sau có là một số chính phương không?
a) 1 mũ 3 + 2 mũ 3
b) 1 mũ 3 + 2 mũ 3 + 3 mũ 3
c) 1 mũ 3 + 2 mũ 3 + 3 mũ 3 + 4 mũ 3
a ) 13 + 23 = 1 + 8 = 9 = 32
Vậy 13 + 23 là một số chính phương
b ) 13 + 23 + 33 = 1 + 8 + 27 = 36 = 62
Vậy 13 + 23 + 33 là một số chính phương
c ) 13 + 23 + 33 + 43 = 1 + 8 + 27 + 64 = 100 = 102
Vậy 13 + 23 + 33 + 43 là một số chính phương
A)13+23=1+8=9=32 la so chinh phuong
B)13+23+33+43=1+8+27=36=62 la so chinh phuong
C)13+23+33+43=1+8+27+64=100=102 la so chinh phuong nhe
chứng minh rằng : tổng lập phương các số tự nhiên liên tiếp từ 1 là một số chính phương: 1 mũ 3 + 2 mũ 3 +..... + n mũ3 =(1+2+.....+n) mũ 2
Giả sử 1^3+2^3+...+n^3=(1+2+...+n)^2(1)
Khi n=1 thì ta sẽ có 1^3=1^2(đúng)
Giả sử (1) đúng khi n=k
Khi n=2 thì ta sẽ có 1^3+2^3=9=(1+2)^2
Ta sẽ cần chứng minh (1) đúng khi n=k+1
1^3+2^3+...+n^3
=1^3+2^3+...+k^3+(k+1)^3
=(1+2+3+...+k)^2+(k+1)^3
Xét biểu thức (k+1)^2+2(k+1)(1+2+...+k)
=(k+1)^2+2*(k+1)*k*(k+1)/2
=(k+1)^2*(1+k)=(k+1)^3
=>1^3+2^3+...+(k+1)^3
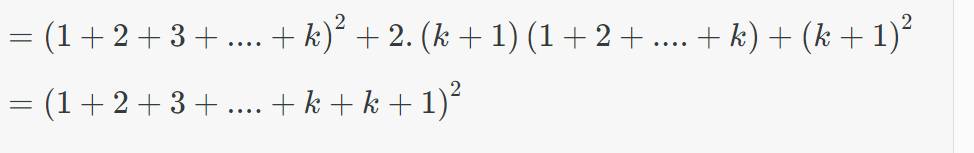
=>ĐPCM
Số chính phương là số bằng bình phương của một số tự nhiên ( ví dụ 0,1,4,9,16...) Mỗi tổng sau có một số chính bằng phương không?
a) 1 mũ 3 + 2 mũ 3
b) 1 mũ 3 + 2 mũ 3 + 3 mũ 3
c) 1 mũ 2 + 2mux 3 + 3 mũ 3 + 4 mũ 3
Số chính phương là số bằng bình phương của một số tự nhiên ( ví dụ: 0,1,4,9,16......). Mỗi tổng sau có là một số chính phương không?
a) 1 mũ 3 + 2 mũ 3
b) 1 mũ 3 + 2 mũ 3 + 3 mũ 3
c) 1 mũ 3 + 2 mũ 3 + 3 mũ 3 + 4 mũ 3
Nhanh nhanh mik tick
a) 1 mũ 3 + 2 mũ 3 bằng 2 mũ 3
b) 1 mũ 3 + 2 mũ 3 + 3 mũ 3 bằng 6 mũ 3
c) 1 mũ 3 + 2 mũ 3 + 3 mũ 3 + 4 mũ 3 bằng 10 mũ 3
Để câu trả lời của bạn nhanh chóng được duyệt và hiển thị, hãy gửi câu trả lời đầy đủ và không nên:
Yêu cầu, gợi ý các bạn khác chọn (k) đúng cho mìnhChỉ ghi đáp số mà không có lời giải, hoặc nội dung không liên quan đến câu hỏi.Các bạn giúp mình bài toán này với ! Nó khó hiểu quá.
Số chính phương là số băng bình phương của một số tự nhiên (ví dụ: 0,1,4,9,16, ...). Mỗi tổng sau có là một số chính phương không ?
a) 1 mũ 3 + 2 mũ 3
b) 1 mũ 3 + 2 mũ 3 + 3 mũ 3
c) 1 mũ 3 + 2 mũ 3 + 3 mũ 3 + 4 mũ 3 .
a) 1^3 + 2^3 = 1+ 8=9 =3^2 là số chính phương
b) 1^3 + 2^3 + 3^3 =1+ 8+ 27=36 =6^2 là số chính phương
c)1^3 + 2^3 +3^3 + 4^3 =1+8+27+64 =100 =10^2 là số chính phương
Vì nó k có quy luật nên cứ tính hết ra nhé!
Chúc bn hok tốt!!!
a. 1 mũ 3 + 2 mũ 3 = (1+2) mũ 2 = 3 mũ 3
b. 1 mũ 3 + 2 mũ 3 + 3 mũ 3 = (1+2+3) mũ 2 = 6 mũ 2
c. 1 mũ 3 +2 mũ 3 + 3 mũ 3 +4 mũ 3 = (1+2+3+4) mũ 2 = 10 mũ 2
Chúc làm tốt
chứng minh rằng tổng lập phương các số tự nhiên liên tiếp từ 1 là một số chính phương : 1+3+5+...+ n mũ 3 =(1+2+...+ n) mũ 2
Đề bài : Chứng minh rằng tổng lập phương của các số tự nhiên liên tiếp từ 1 đến n bằng bình phương của tổng từ 1 đến n ( n tự nhiên ). Hay ta cần chứng minh : \(1^3+2^3+3^3+4^3+....+n^3=\left(1+2+....+n\right)^2\) (*)
Lời giải :
+) Xét \(n=1\) thì ta có : \(1^3=1^2\) ( đúng )
Suy ra (*) đúng với \(n=1\) (1)
+) Xét \(n=2\) ta có : \(1^3+2^3=1+8=9\); \(\left(1+2\right)^2=3^2=9\)
\(\Rightarrow1^3+2^3=\left(1+2\right)^2\) ( đúng ). Nên (*) đúng với \(n=2\) (2)
+) Giả sử (*) đúng với \(n=k\). Tức là : \(1^3+2^3+3^3+....+k^3=\left(1+2+...+k\right)^2\).
Ta cần chứng minh \(n=k+1\) cũng đúng với (*). Thật vậy , ta có :
\(1^3+2^3+3^3+.....+\left(k+1\right)^3\)
\(=1^3+2^3+....+k^3+\left(k+1\right)^3\)
\(=\left(1+2+3+....+k\right)^2+\left(k+1\right)^3\)
Xét biểu thức \(\left(k+1\right)^2+2.\left(k+1\right).\left(1+2+3+....+k\right)\)
\(=\left(k+1\right)^2+2.\left(k+1\right)\cdot\frac{\left(k+1\right).k}{2}\)
\(=\left(k+1\right)^2+\left(k+1\right)^2.k=\left(k+1\right)^3\)
Do đó \(1^3+2^3+....+\left(k+1\right)^3\)
\(=\left(1+2+3+....+k\right)^2+2.\left(k+1\right)\left(1+2+....+k\right)+\left(k+1\right)^2\)
\(=\left(1+2+3+....+k+k+1\right)^2\)
Vậy (*) đúng với \(n=k+1\) (3)
Từ (1) (2) và (3) suy ra \(1^3+2^3+3^3+4^3+....+n^3=\left(1+2+....+n\right)^2\) với mọi \(n\in N\).
Cho P= 14 mũ 14 mũ 14+9 mũ 9 mũ 9+2 mũ 3 mũ 4. Chứng minh rằng P không phải là số chính phương
Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.
Cho P= 14 mũ 14 mũ 14+9 mũ 9 mũ 9+2 mũ 3 mũ 4. Chứng minh rằng P không phải là số chính phương