Question

chứng minh rằng : tổng lập phương các số tự nhiên liên tiếp từ 1 là một số chính phương:           1 mũ 3 + 2 mũ 3 +..... + n mũ3 =(1+2+.....+n) mũ 2

Answer 1

Giả sử 1^3+2^3+...+n^3=(1+2+...+n)^2(1)

Khi n=1 thì ta sẽ có 1^3=1^2(đúng)

Giả sử (1) đúng khi n=k

Khi n=2 thì ta sẽ có 1^3+2^3=9=(1+2)^2

Ta sẽ cần chứng minh (1) đúng khi n=k+1

1^3+2^3+...+n^3

=1^3+2^3+...+k^3+(k+1)^3

=(1+2+3+...+k)^2+(k+1)^3

Xét biểu thức (k+1)^2+2(k+1)(1+2+...+k)

=(k+1)^2+2*(k+1)*k*(k+1)/2

=(k+1)^2*(1+k)=(k+1)^3

=>1^3+2^3+...+(k+1)^3

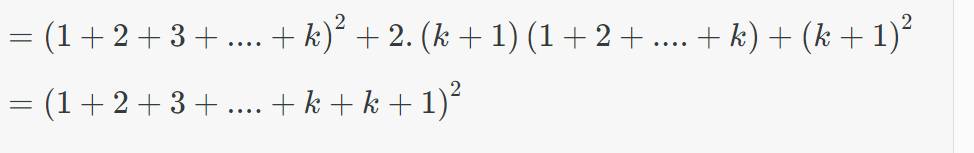
=>ĐPCM