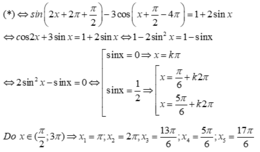1, \(y=2-sin\left(\dfrac{3x}{2}+x\right).cos\left(x+\dfrac{\pi}{2}\right)\)

 \(y=2-\left(-cosx\right).\left(-sinx\right)\)

y = 2 - sinx.cosx

y = \(2-\dfrac{1}{2}sin2x\)

Max = 2 + \(\dfrac{1}{2}\) = 2,5

Min = \(2-\dfrac{1}{2}\) = 1,5

2, y = \(\sqrt{5-\dfrac{1}{2}sin^22x}\)

Min = \(\sqrt{5-\dfrac{1}{2}}=\dfrac{3\sqrt{2}}{2}\)

Max = \(\sqrt{5}\)

a, \(y=sin^2x-2sinx+3cos^2x\)

\(=sin^2x-2sinx+3\left(1-sin^2x\right)\)

\(=3-2sinx-2sin^2x\)

Đặt \(sinx=t\left(t\in\left[0;1\right]\right)\)

\(\Rightarrow y=f\left(t\right)=3-2t-2t^2\)

\(\Rightarrow y_{min}=min\left\{f\left(0\right);f\left(1\right)\right\}=-1\)

\(y_{max}=max\left\{f\left(0\right);f\left(1\right)\right\}=3\)

b, \(y=sinx-cosx+sin2x+5\)

\(=sinx-cosx-\left(sinx-cosx\right)^2+6\)

Đặt \(sinx-cosx=t\left(t\in\left[-\sqrt{2};\sqrt{2}\right]\right)\)

\(\Rightarrow y=f\left(t\right)=-t^2+t+6\)

\(\Rightarrow y_{min}=min\left\{f\left(-\sqrt{2}\right);f\left(0\right)\right\}=4-\sqrt{2}\)

\(y_{max}=max\left\{f\left(-\sqrt{2}\right);f\left(0\right)\right\}=6\)

c, \(y=sinx-cosx+sinx.cosx-3\)

\(=sinx-cosx-\dfrac{1}{2}\left(sinx-cosx\right)^2-\dfrac{5}{2}\)

Đặt \(sinx-cosx=t\left(t\in\left[-\sqrt{2};\sqrt{2}\right]\right)\)

\(\Rightarrow y=f\left(t\right)=-\dfrac{1}{2}t^2+t-\dfrac{5}{2}\)

\(\Rightarrow y_{min}=min\left\{f\left(-\sqrt{2}\right);f\left(\sqrt{2}\right);f\left(1\right)\right\}=-\dfrac{7+2\sqrt{2}}{2}\)

\(y_{max}=max\left\{f\left(-\sqrt{2}\right);f\left(\sqrt{2}\right);f\left(1\right)\right\}=-2\)

a.

\(y=2\left(1-cos2x\right)-\dfrac{5}{2}sin2x+\dfrac{1}{2}+\dfrac{1}{2}cos2x+10\)

\(=-\dfrac{1}{2}\left(5sin2x+3cos2x\right)+\dfrac{25}{2}\)

\(=-\dfrac{\sqrt{34}}{2}\left(\dfrac{5}{\sqrt{34}}sin2x+\dfrac{3}{\sqrt{34}}cos2x\right)+\dfrac{25}{2}\)

Đặt \(\dfrac{5}{\sqrt{34}}=cosa\)

\(\Rightarrow y=-\dfrac{\sqrt{34}}{2}\left(sin2x.cosa+cos2x.sina\right)+\dfrac{25}{2}\)

\(=-\dfrac{\sqrt{34}}{2}sin\left(2x+a\right)+\dfrac{25}{2}\)

Do \(-1\le sin\left(2x+a\right)\le1\)

\(\Rightarrow\dfrac{25-\sqrt{34}}{2}\le y\le\dfrac{25+\sqrt{34}}{2}\)

b.

\(y=\dfrac{sin^2x-2sin2x+1}{3+sin^2x+2cos^2x}=\dfrac{2sin^2x-4sin2x+2}{6+2\left(sin^2x+cos^2x\right)+2cos^2x}\)

\(=\dfrac{1-cos2x-4sin2x+2}{8+1+cos2x}=\dfrac{3-4sin2x-cos2x}{9+cos2x}\)

\(\Rightarrow9y+y.cos2x=3-4sin2x-cos2x\)

\(\Rightarrow4sin2x+\left(y+1\right)cos2x=3-9y\)

Theo điều kiện có nghiệm của pt lượng giác bậc nhất:

\(4^2+\left(y+1\right)^2\ge\left(3-9y\right)^2\)

\(\Leftrightarrow80y^2-56y-8\le0\)

\(\Rightarrow\dfrac{7-\sqrt{89}}{20}\le y\le\dfrac{7+\sqrt{89}}{20}\)

c.

\(y=2sinx+3cosx+4\)

\(=\sqrt{13}\left(\dfrac{2}{\sqrt{13}}sinx+\dfrac{3}{\sqrt{13}}cosx\right)+4\)

Đặt \(\dfrac{2}{\sqrt{13}}=cosa\)

\(\Rightarrow y=\sqrt{13}\left(sinx.cosa+cosx.sina\right)+4\)

\(=\sqrt{13}sin\left(x+a\right)+4\)

Do \(-1\le sin\left(x+a\right)\le1\)

\(\Rightarrow-\sqrt{13}+4\le y\le\sqrt{13}+4\)

Câu 3 sai đề hả bạn

\(y=sin\left(x+\dfrac{\pi}{3}\right)-sinx\)

\(=\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx-sinx\)

\(=\dfrac{\sqrt{3}}{2}cosx-\dfrac{1}{2}sinx\)

\(=cos\left(x+\dfrac{\pi}{6}\right)\in\left[-1;1\right]\)

\(\Rightarrow\left\{{}\begin{matrix}y_{mịn}=-1\Leftrightarrow x=\dfrac{5\pi}{6}+k2\pi\\y_{max}=1\Leftrightarrow x=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)

Đáp án C

a.

\(y'=\dfrac{2-x}{2x^2\sqrt{x-1}}=0\Rightarrow x=2\)

\(y\left(1\right)=0\) ; \(y\left(2\right)=\dfrac{1}{2}\) ; \(y\left(5\right)=\dfrac{2}{5}\)

\(\Rightarrow y_{min}=y\left(1\right)=0\)

\(y_{max}=y\left(2\right)=\dfrac{1}{2}\)

b.

\(y'=\dfrac{1-3x}{\sqrt{\left(x^2+1\right)^3}}< 0\) ; \(\forall x\in\left[1;3\right]\Rightarrow\) hàm nghịch biến trên [1;3]

\(\Rightarrow y_{max}=y\left(1\right)=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)

\(y_{min}=y\left(3\right)=\dfrac{6}{\sqrt{10}}=\dfrac{3\sqrt{10}}{5}\)

c.

\(y=1-cos^2x-cosx+1=-cos^2x-cosx+2\)

Đặt \(cosx=t\Rightarrow t\in\left[-1;1\right]\)

\(y=f\left(t\right)=-t^2-t+2\)

\(f'\left(t\right)=-2t-1=0\Rightarrow t=-\dfrac{1}{2}\)

\(f\left(-1\right)=2\) ; \(f\left(1\right)=0\) ; \(f\left(-\dfrac{1}{2}\right)=\dfrac{9}{4}\)

\(\Rightarrow y_{min}=0\) ; \(y_{max}=\dfrac{9}{4}\)

d.

Đặt \(sinx=t\Rightarrow t\in\left[-1;1\right]\)

\(y=f\left(t\right)=t^3-3t^2+2\Rightarrow f'\left(t\right)=3t^2-6t=0\Rightarrow\left[{}\begin{matrix}t=0\\t=2\notin\left[-1;1\right]\end{matrix}\right.\)

\(f\left(-1\right)=-2\) ; \(f\left(1\right)=0\) ; \(f\left(0\right)=2\)

\(\Rightarrow y_{min}=-2\) ; \(y_{max}=2\)