Giải câu 1 tự luận giùm mình 

Những câu hỏi liên quan
Giải tự luận giùm mình
Giải lý tự luận và tóm tắt giùm mình nha
Tìm số tự nhiên x , biết :
a, 2/3 = x/54
b, 10/x = 15/6
c, 2/3 < x/6 < 1
d, 1 < 6/x < 2
Mọi người giải chi tiết giùm mình nha nhớ là phải có câu lập luận nữa nhé
\(a,\frac{2}{3}=\frac{x}{54}\)
\(\Rightarrow2.54=3x\)
\(\Rightarrow3x=108\)
\(\Rightarrow x=108:3=36\)
\(b,\frac{10}{x}=\frac{15}{6}\)
\(\Rightarrow10.6=15x\)
\(\Rightarrow15x=60\)
\(\Rightarrow x=60:15=4\)
\(c,\frac{2}{3}< \frac{x}{6}< 1\)
\(\Rightarrow\frac{4}{6}< \frac{x}{6}< \frac{6}{6}\)
\(\Rightarrow4< x< 6\)
\(\Rightarrow x=5\)
\(d,1< \frac{6}{x}< 2\)
\(\Rightarrow\frac{6}{6}< \frac{6}{x}< \frac{6}{3}\)
\(\Rightarrow6< x< 3\)
\(\Rightarrow x=5;4\)
Đúng 0
Bình luận (0)
a)x=54.2:3=36
b)x=10.6:15=4
c)x = 5
d)x=4 hoặc x=5
Đúng 0
Bình luận (0)
a, ta nhan mau so 3 len bang voi 54 => 2/3= 2.(54:3)/54:3= 2.18/18= 36/18
2.36/3.18= 72/54 .suy ra x = 72
b,10/x= 10.6/6.x= 60/6.x , ma
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải tin tự luận giùm
Bài 2:
#include <bits/stdc++.h>
using namespace std;
double a,b,c,delta,x1,x2;
int main()
{
//freopen("PTB2.inp","r",stdin);
//freopen("PTB2.out","w",stdout);
cin>>a>>b>>c;
delta=(b*b-4*a*c);
if (delta<0) cout<<"-1";
if (delta==0) cout<<fixed<<setprecision(5)<<(-b/(2*a));
if (delta>0)
{
x1=(-b-sqrt(delta))/(2*a);
x2=(-b+sqrt(delta))/(2*a);
cout<<fixed<<setprecision(5)<<x1<<" "<<fixed<<setprecision(5)<<x2;
}
return 0;
}
Đúng 1
Bình luận (0)
Giải ra tự luận giùm em ạ
Câu 18:
Ta có: \(3\sqrt{8a}+\dfrac{1}{4}\sqrt{\dfrac{32a}{25}}-\dfrac{a}{\sqrt{3}}\cdot\sqrt{\dfrac{3}{2a}}-\sqrt{2a}\)
\(=6\sqrt{2a}-\sqrt{2a}+\dfrac{1}{4}\cdot\dfrac{4\sqrt{2a}}{5}-\dfrac{a}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{\sqrt{2a}}\)
\(=5\sqrt{2a}+\dfrac{1}{5}\sqrt{2a}-\dfrac{1}{2}\sqrt{2a}\)
\(=\dfrac{47}{10}\sqrt{2a}\)
Chọn C
Đúng 1
Bình luận (0)
Câu 18
\(=3\sqrt{4}.\sqrt{2a}+\frac{1}{4}\sqrt{\frac{16}{25}}.\sqrt{2a}-\sqrt{\frac{a^2}{3}}.\sqrt{\frac{3}{2a}}-\sqrt{2a}\)
\(=6\sqrt{2a}+\frac{1}{5}\sqrt{2a}-\sqrt{\frac{a}{2}}-\sqrt{2a}\)
\(=6\sqrt{2a}+\frac{1}{5}\sqrt{2a}-\sqrt{\frac{1}{4}}.\sqrt{2a}-\sqrt{2a}\)
\(=6\sqrt{2a}+\frac{1}{5}\sqrt{2a}-\frac{1}{2}\sqrt{2a}-\sqrt{2a}=\frac{47}{10}\sqrt{2a}\)
Đáp án C.
Đúng 0
Bình luận (0)
Câu 19:
\(=2\sqrt{a}-\sqrt{(3a)^2}.\sqrt{a}+a\sqrt{a}.\sqrt{16}+\sqrt{\frac{4}{a^4}.36a^5}\)
\(=2\sqrt{a}-3a\sqrt{a}+4a\sqrt{a}+\sqrt{144a}\)
\(=2\sqrt{a}+a\sqrt{a}+\sqrt{144}.\sqrt{a}=2\sqrt{a}+a\sqrt{a}+12\sqrt{a}=14\sqrt{a}+a\sqrt{a}\)
Đáp án A.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giúp toán tự luận giùm mình
Câu 1:
\(f\left(-x\right)=\left(-x\right)^4-3\cdot\left(-x\right)^2+1\)
\(=x^4-3x^2+1=f\left(x\right)\)
Vậy: f(x) là hàm số chẵn
Đúng 1
Bình luận (1)
\(c1:D=R\Rightarrow\forall x\in D\Rightarrow-x\in D\)
\(\Rightarrow f\left(-x\right)=x^4-3x^2+1=f\left(x\right)\Rightarrow hàm\) \(số\) \(chẵn\)
\(c2:cm:\overrightarrow{AC}+\overrightarrow{BD}=2\overrightarrow{MN}\)
\(M,N\) \(trung\) \(điểm\) \(AB,CD\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}\\\overrightarrow{DN}+\overrightarrow{CN}=\overrightarrow{0}\end{matrix}\right.\)
\(\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}\)
\(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}\)
\(\Rightarrow2\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{MA}+\overrightarrow{BC}+\overrightarrow{AD}+\overrightarrow{CN}+\overrightarrow{DN}\)
\(=\overrightarrow{0}+\overrightarrow{BC}+\overrightarrow{AD}+\overrightarrow{0}\Rightarrow2\overrightarrow{MN}=\overrightarrow{AD}+\overrightarrow{BC}\left(đpcm\right)\)
\(c3:D=R\text{[}-5;\text{+∞.)}\)
\(f\left(x\right)\) \(nghịch\) \(biến\Leftrightarrow a< 0\)
\(\Rightarrow-5\le a< 0\left(a\in Z\right)\Rightarrow a=\left\{-5;-4;-3;-2;-1\right\}\)
\(c4:\) có công thức \(X\cap Y=X+Y-X\cup Y=25+20-36=9\)
Đúng 0
Bình luận (0)


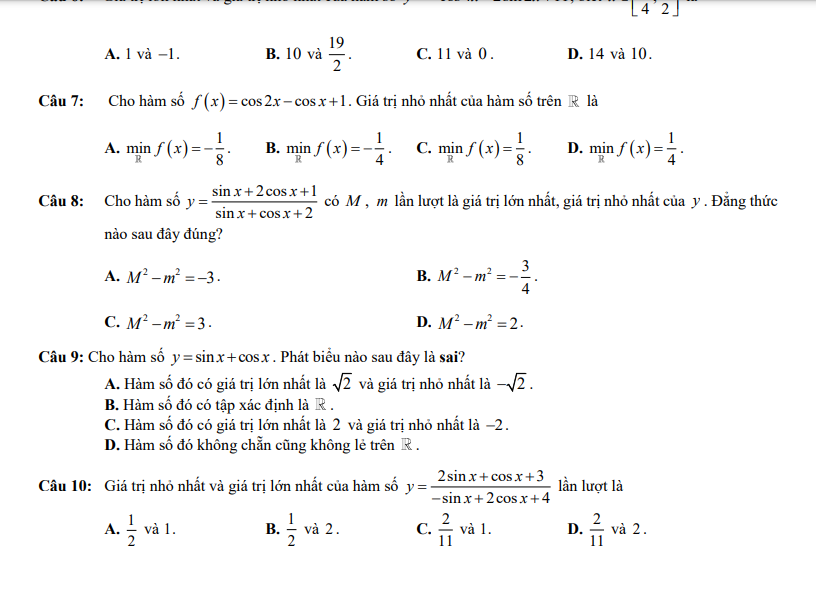
giải giùm em theo kiểu tự luận ạ
1.
\(2sinx+cosx=4\)
\(\Leftrightarrow\sqrt{5}\left(\dfrac{2}{\sqrt{5}}sinx+\dfrac{1}{\sqrt{5}}cosx\right)=4\)
\(\Leftrightarrow sin\left(x+arccos\dfrac{2}{\sqrt{5}}\right)=\dfrac{4}{\sqrt{5}}>1\)
\(\Rightarrow2sinx+4cosx-4\ne0\)
Khi đó:
\(2P.sinx+P.cosx-4P=sinx-2cosx-3\)
\(\Leftrightarrow\left(2P-1\right)sinx+\left(P+2\right)cosx=4P-3\)
Phương trình có nghiệm khi:
\(\left(2P-1\right)^2+\left(P+2\right)^2\ge\left(4P-3\right)^2\)
\(\Leftrightarrow4P^2-4P+1+P^2+4P+4\ge16P^2+9-24P\)
\(\Leftrightarrow11P^2-24P+4\le0\)
\(\Leftrightarrow\dfrac{2}{11}\le P\le2\)
\(\Rightarrow maxP=2\)
Đúng 2
Bình luận (0)

giải giúp mình câu tự luận ạ
Để đánh số trang của một cuốn sách có 136 trang cần dùng tất cả bao nhiêu chữ số 2? Giải tự luận giùm mình cảm ơn mọi người nhiều!
tải quanda về nha
Giúp mình làm! Câu 2 giải tự luận chi tiết giúp mình
2.
Xét BPT: \(\left(x+3\right)\left(4-x\right)>0\Leftrightarrow-3< x< 4\) \(\Rightarrow D_1=\left(-3;4\right)\)
Xét BPT: \(x< m-1\) \(\Rightarrow D_2=\left(m-1;+\infty\right)\)
Hệ có nghiệm khi và chỉ khi \(D_1\cap D_2\ne\varnothing\)
\(\Leftrightarrow m-1< 4\)
\(\Leftrightarrow m< 5\)
3.
\(\dfrac{\pi}{24}=\dfrac{180^0}{24}=7^030'\)
4.
\(x^2+y^2-x+y+4=0\) không phải đường tròn
Do \(\left(\dfrac{1}{2}\right)^2+\left(-\dfrac{1}{2}\right)^2-4< 0\)
Đúng 0
Bình luận (0)
5.
\(f\left(x\right)=ax^2+bx+c\) có \(\left\{{}\begin{matrix}a\ne0\\\Delta=b^2-4ac< 0\end{matrix}\right.\) thì \(f\left(x\right)\) không đổi dấu trên R
6.
\(sin2020a=sin\left(2.1010a\right)=2sin1010a.cos1010a\)
7.
Công thức B sai
\(cos^2a+sin^2a=1\) , không phải \(cos2a\)
Đúng 0
Bình luận (0)


















