Tìm Min C = x12 _ 4x3 + 2018

Những câu hỏi liên quan
Tìm GTLN (max), GTNN (min) của
y
4
x
3
-
3
x
khi
x
∈
-
1
;
2
Đọc tiếp
Tìm GTLN (max), GTNN (min) của y = 4 x 3 - 3 x khi x ∈ - 1 ; 2
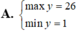
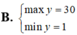
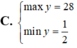
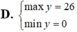
Cho pt bậc x2 - (3m-1)x + 2m2 + m - 1=0 (m là tham số)
a) Giải pt khi m= -1
b) Giả sử x12 , x22 là hai nghiệm pb của chương trình. Tìm m để B= x12 - x22 - 3x1x2 đạt min
a: Khi m=-1 thì phương trình sẽ là:
x^2-(-3-1)x+2-1-1=0
=>x^2+4x=0
=>x=0 hoặc x=-4
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức: A = |x - 2017| + |x+2018|
A. min A = 1 B. min A = 4035
C. min A = 2017 D. min A = 2018
tìm min của :
\(C=\frac{|x-2017|+2018}{|x-2017|+2019}\)
\(C=\frac{\left|x-2017\right|+2018}{\left|x-2017\right|+2019}=\frac{\left|x-2017\right|+2019-1}{\left|x-2017\right|+2019}=1-\frac{1}{\left|x-2017\right|+2019}\)
C nhỏ nhất => \(\frac{1}{\left|x-2017\right|+2019}\)lớn nhất
=> |x+2017|+2019 nhỏ nhất
\(\left|x+2017\right|\ge0\Rightarrow\left|x+2017\right|+2019\ge2019\)
dấu = xảy ra khi |x+2017|=0
=> x=-2017
Vậy MIN C=\(\frac{2018}{2019}\)
p/s: :)) có vẻ ko hoàn hảo lắm
Đúng 0
Bình luận (0)
tìm min A=/2x-2017/+/2x-2018/
Ta có:
\(\left|2x-2017\right|\ge2x-2017\forall x\)
\(\left|2x-2018\right|=\left|2018-2x\right|\ge2018-2x\forall x\)
\(\Rightarrow\left|2x-2017\right|-\left|2x-2018\right|\ge1\)
Dấu "=" xảy ra khi
\(\hept{\begin{cases}2x-2017\ge0\\2x-2018\le0\end{cases}\Rightarrow\hept{\begin{cases}x\ge\frac{2017}{2}\\x\le\frac{2018}{2}\end{cases}}}\)
Đúng 0
Bình luận (0)
Tìm Max,Min của
A= \(x\left(2018+\sqrt{2020-x^2}\right)\)
Tìm Min của A=(x^2-2*x+2018)/x^2
Ta có \(\frac{x^2-2x+2018}{x^2}=1-\frac{2}{x}+\frac{2018}{x^2}=2018\left(\frac{1}{x^2}-\frac{2}{2018x}+\frac{1}{2018}\right)=2018\left(\frac{1}{x^2}-2.\frac{1}{2018x}+\frac{1}{2018^2}\right)+\frac{2017}{2018}=2018.\left(\frac{1}{x}-\frac{1}{2018}\right)^2+\frac{2017}{2018}\)
Nhận thấy \(2018\left(\frac{1}{x}-\frac{1}{2018}\right)^2\ge0\forall x=>2018\left(\frac{1}{x}-\frac{1}{2018}\right)^2+\frac{2017}{2018}\ge\frac{2017}{2018}\forall x\)
Dấu "=" xảy ra khi 1/x-1/2018=0=> x=2018
Vậy min A=2017/2018 <=> x=2018
Đúng 0
Bình luận (0)
Cho a;b >0 ;2017/a + 2018/b =1 tìm min a+b
Lời giải:
Áp dụng BĐT Cauchy-Schwarz:
\(1=\frac{2017}{a}+\frac{2018}{b}\geq \frac{(\sqrt{2017}+\sqrt{2018})^2}{a+b}\)
\(\Rightarrow a+b\geq (\sqrt{2017}+\sqrt{2018})^2\)
Vậy $a+b$ min $=(\sqrt{2017}+\sqrt{2018})^2$
Đúng 0
Bình luận (0)
Tìm min:
\(C=x^2-4x+16\)
\(D=2x^2+9y^2-6xy-8x-12y+2018\)
C = x2 - 4x + 16
= (x2 - 4x + 4) + 12
= (x - 2)2 + 12
Vậy Cmin = 12 (vì \(\left(x-2\right)^2\ge0\Leftrightarrow\left(x-2\right)^2+12\ge12\))
Còn D mình không biết cách làm
Đúng 0
Bình luận (0)
Thôi em làm luôn nha:)
\(D=\left(x^2-2.x.3y+9y^2\right)+4\left(x-3y\right)+4+x^2-2.x.6+36+1978\)
\(=\left(x-3y\right)^2+2\left(x-3y\right).2+2^2+\left(x-6\right)^2+1978\)
\(=\left(x-3y+2\right)^2+\left(x-6\right)^2+1978\ge1978\)
Đẳng thức xảy ra x =6, y = 8/3
Đúng 0
Bình luận (0)






















