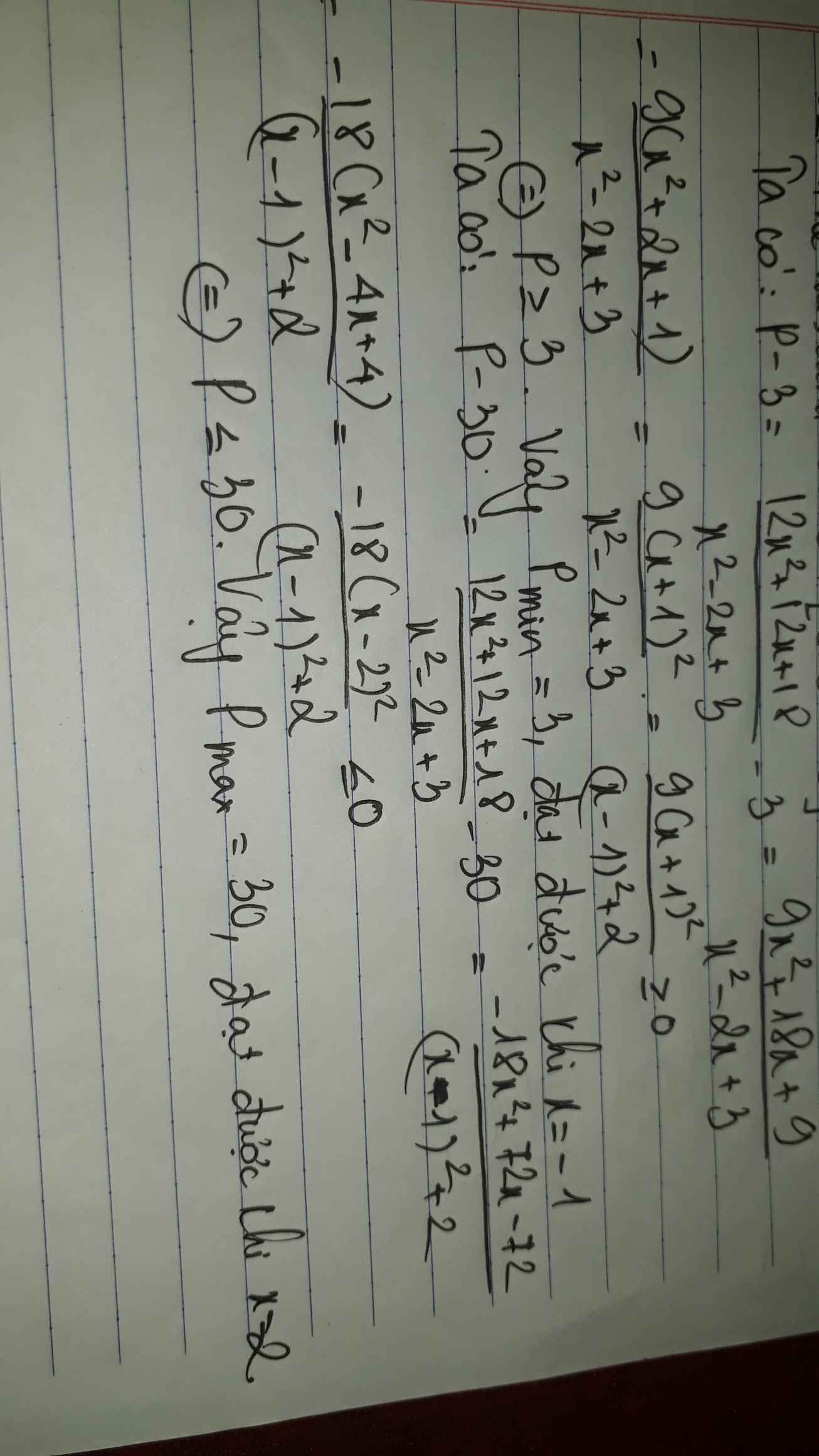\(A=x^2-12x+18\)

\(A=x^2-2.x.6+36-36+18\)

\(A=\left(x-6\right)^2-18\)

Vì \(\left(x-6\right)^2\ge0\)

Nên \(\left(x-6\right)^2-18\ge-18\)

Vậy \(A_{MIN}=-18\Leftrightarrow x-6=0\Leftrightarrow x=6\)

Ta có : \(A=x^2-12x+18\)

                 \(=x^2-2.x.6+6^2-18\)

                  \(=\left(x-6\right)^2-18\)

Có : \(\left(x-6\right)^2\ge0\)

\(\Rightarrow\left(x-6\right)^2-18\ge-18\)

Dấu " = " xảy ra khi \(x-6=0\)

                                   \(x=6\)

Vậy \(MIN_A=-18\) khi \(x=6\)

A= x² - 12x + 18

=x² - 12x + 36-18

=(x-6)²-18\(\ge\)-18

Dấu = khi x=6

Vậy MinA=-18 khi x=6

Chọn B

Bạn lưu ý chỉ đăng bài MỘT LẦN thôi chứ không đăng lặp lại gây loãng trang web.

Lời giải:

a. Ta thấy:

$18x-30y=3(6x-10y)$ chia hết cho $3$ với mọi $x,y$ nguyên, mà $59$ không chia hết cho $3$

Do đó pt $18x-30y=59$ vô nghiệm.

b. $22x-5y=77$

$5y=22x-77=11(2x-7)\vdots 11$

$\Rightarrow y\vdots 11$. Đặt $y=11k$ với $k$ nguyên 

$22x-55k=77$

$2x-5k=7$

$2x=5k+7\vdots 2$

$\Rightarrow k$ lẻ. Đặt $k=2t+1$ với $t$ nguyên

$2x=5(2t+1)+7=10t+12$

$x=5t+6$

Vậy $(x,y)=(5t+6, 22t+11)$ với $t$ nguyên 

c.

$12x+19y=94$

$19y=94-12x\vdots 2\Rightarrow y\vdots 2$

Đặt $y=2k$ với $k$ nguyên. Khi đó:

$12x+38k=94$

$6x+19k=47$

$6k=47-19k=19(2-k)+9$

$\Rightarrow 6k-9\vdots 19$

$\Leftrightarrow 2k-3\vdots 19$

$\Leftrightarrow 2k-22\vdots 19$

$\Leftrightarrow k-11\vdots 19$

$\Rightarrow k=19t+11$ với $t$ nguyên

 \(x=\frac{47-19k}{6}=\frac{47-19(19t+11)}{6}=\frac{-162-361t}{6}=-27-\frac{361t}{6}\)

Để $x$ nguyên thì $t\vdots 6$. Khi đó đặt $t=6m$ với  $m$ nguyên 

Khi đó:

$y=2k=2(19t+11)=2(114m+11)=228m+22$

$x=-27-361m$ với $m$ nguyên bất kỳ.