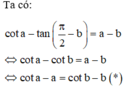Cho tan(a+b)=7 , tan(a-b)=4 . Khi đó , giá trị của tan2a là

Những câu hỏi liên quan
Cho π/2 < a < 3π/4. Giá trị tan2a là
A. -2 7 B. 3 3 /4
C. -3 7 D. 3 7
Với π/2 < a < 3π/4 thì cosa < 0. Ta có
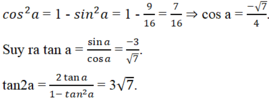
Đáp án là D.
Đúng 0
Bình luận (0)
Cho \(tan\left(a+b\right)=5\); \(tan\left(a-b\right)=4\). Tìm \(tan2a\)
\(tan2a=tan\left[\left(a+b\right)+\left(a-b\right)\right]=\dfrac{tan\left(a+b\right)+tan\left(a-b\right)}{1-tan\left(a+b\right)tan\left(a-b\right)}\)
\(\Rightarrow\dfrac{tan\left(a+b\right)+tan\left(a-b\right)}{1-tan\left(a+b\right)tan\left(a-b\right)}=\dfrac{5+4}{1-5.4}=-\dfrac{9}{19}\)
Vậy \(tan2a=-\dfrac{9}{19}\)
Đúng 0
Bình luận (1)
Cho Tan a= 2.Khi đó giá trị của E= sin^2 a - sin a cos a bằng bao nhiêu
A. 0,4 B 0,2 C 0,3 D 0,5
Cho tan2a = 4/3 với π/2 < a < π. Giá trị cos a là

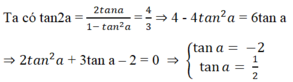
Vì π/2 < a < π nên tan a < 0, do đó tan a = -2.
Áp dụng công thức
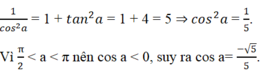
Đáp án là B.
Đúng 0
Bình luận (0)
Cho hai góc nhọn a và b với tan a = 1/7 và tan b = 3/4. Tính tổng 2 góc đó?
![]()
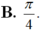
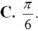
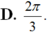
Chọn B.
Theo công thức cộng ta có:
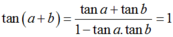
Mà a và b là các góc nhọn suy ra 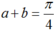
Đúng 0
Bình luận (0)
Tam giác ABC thỏa mãn điều kiện : \(\tan A,\tan B,\tan C\) theo thứ tự đó lập thành cấp số cộng. Hãy tìm giá trị nhỏ nhất của góc B có thể có được ?
Theo giả thiết \(\tan A,\tan B,\tan C\) lập thành cấp số cộng thì ta có : \(\tan A+\tan C=2\tan B\)
\(\Leftrightarrow\tan A+\tan C=\frac{\sin\left(A+C\right)}{\cos A.\cos C}=\frac{\sin B}{\cos A.\cos C}\Rightarrow\frac{2\sin B}{\cos B}=\frac{\sin B}{\cos A.\cos C}\)
\(\Leftrightarrow\frac{2}{\cos B}=\frac{1}{\cos A.\cos C}\Leftrightarrow2\cos A.\cos C=\cos B\)
\(\Leftrightarrow\cos\left(A+C\right)+\cos\left(A-C\right)=\cos B\)
\(\Leftrightarrow-\cos B+\cos\left(A-C\right)=\cos B\Leftrightarrow\cos B=\frac{1}{2}\cos\left(A-C\right)\le\frac{1}{2}\left(2\right)\)
( Vì \(0 <\)\(\cos\left(A-C\right)\le1\) )
Do 0 < B \(\le\pi\Rightarrow\) giá trị nhỏ nhất của \(B=\frac{\pi}{3}\)
Đúng 0
Bình luận (0)
Cho a, b là các số thực thuộc khoảng
0
;
π
2
và thỏa mãn điều kiện
c
o
t
a
-
tan
π
2
-
b
a
-
b
.Tính giá trị của biểu thức
P
3...
Đọc tiếp
Cho a, b là các số thực thuộc khoảng 0 ; π 2 và thỏa mãn điều kiện c o t a - tan π 2 - b = a - b .Tính giá trị của biểu thức P = 3 a + 7 b a + b
A. P=5
B. P=2
C. P=4
D. P=6
Biết sina = -4/5 với 3π/4 < a < π. Giá trị tan a là
A. 1/2 B. 2
C. -2 D. -1/2
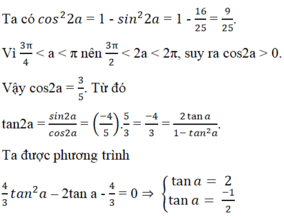
Vì 3π/4 < a < π nên tan a < 0. Vậy tan a = (-1)/2. Đáp án là D.
Đúng 0
Bình luận (0)
Bài 2. (2,0 điểm): Hoà tan 4,6 gam Na trong nước cất thu được V lit Hạ (đktc) và dung dịch A chứa
m gam chat tan
a) Viết phương trình hóa học của phản ứng xảy ra.
b) Tim giá trị của V, m
c) Nêu hiện tượng khi nhúng quỳ tim vào dung dịch A.
(Cho nguyên tử khối (đvC) của Na23, O16 H1)
Câu 3: (1đ)
Bảng sau đây cho biết lượng chất rắn hòa tan tối đa của đường tinh luyện trong 100 ml nước cất ở các
nhiệt độ khác nhau.
Nhiệt độ (C)
20
40
60
80
100
Khôi lượng chất răn(g)|
2019
235,6|...
Đọc tiếp
Bài 2. (2,0 điểm): Hoà tan 4,6 gam Na trong nước cất thu được V lit Hạ (đktc) và dung dịch A chứa m gam chat tan a) Viết phương trình hóa học của phản ứng xảy ra. b) Tim giá trị của V, m c) Nêu hiện tượng khi nhúng quỳ tim vào dung dịch A. (Cho nguyên tử khối (đvC) của Na=23, O=16 H=1) Câu 3: (1đ) Bảng sau đây cho biết lượng chất rắn hòa tan tối đa của đường tinh luyện trong 100 ml nước cất ở các nhiệt độ khác nhau. Nhiệt độ (C) 20 40 60 80 100 Khôi lượng chất răn(g)| 2019 235,6| 288,8 | 365,1 476.0 | a) Vẽ đồ thị biểu diễn mối quan hệ giữa lượng đường hòa tan và nhiệt độ của nước. b) Từ đô thị ở trên, nhận xét mối quan hệ giữa độ tan của đường với nhiệt độ.
Bài 2:
\(n_{Na}=\dfrac{4,6}{23}=0,2\left(mol\right)\\a, 2Na+2H_2O\rightarrow2NaOH+H_2\\ b,n_{H_2}=\dfrac{0,2}{2}=0,1\left(mol\right)\\ V_{H_2\left(đktc\right)}=0,1.22,4=2,24\left(l\right)\\ c,NaOH:Tính.bazo\Rightarrow Quỳ.tím.hoá.xanh\)
Đúng 0
Bình luận (0)
Câu 3: Em chụp lại bảng nha
Đúng 0
Bình luận (1)