b: Xét tứ giác ABDC có 

M là trung điểm của AD
M là trung điểm của BC

Do đó: ABDC là hình bình hành

Suy ra: CD//AB

a: Xét ΔAMB và ΔDMC có

MA=MD

\(\widehat{AMB}=\widehat{DMC}\)

MB=MC

Do đó: ΔAMB=ΔDMC

Huhu mình cần gấp ạa 

a: Xét ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

Do đó: ΔAMB=ΔAMC

b: Xét ΔMAC và ΔMDB có

MA=MD

\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)

MC=MB

Do đó: ΔMAC=ΔMDB

=>\(\widehat{MAC}=\widehat{MDB}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AC//BD

c: Xét ΔIAM và ΔKDM có

IA=KD

\(\widehat{IAM}=\widehat{KDM}\)

AM=DM

Do đó: ΔIAM=ΔKDM

=>\(\widehat{IMA}=\widehat{KMD}\)

mà \(\widehat{IMA}+\widehat{IMD}=180^0\)(hai góc kề bù)

nên \(\widehat{KMD}+\widehat{IMD}=180^0\)

=>K,M,I thẳng hàng

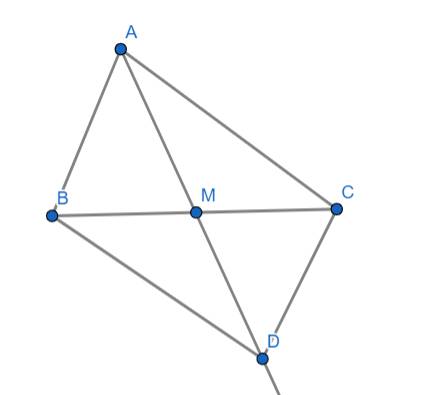
a) Xét ΔAMB và ΔDMC có:

\(AM=CM\) (gt) 

\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh) 

\(BM=CM\) (M là trung điểm của BC) 

\(\Rightarrow\text{Δ}AMB=\text{Δ}DMC\left(c.g.c\right)\)

b) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)

\(\Rightarrow AB=DC\) (2 cạnh t.ứng)  

c) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)

\(\Rightarrow\widehat{MAB}=\widehat{MDC}\) (hai góc t.ứng) 

Mà hai góc này ở vị trí so le trong 

\(\Rightarrow AB//CD\)

Ôi xin lỗi nhé,nhưng mình không hiểu cái đề bài cho lắm!

không sao

a) Xét tam giác AMB và tam giác DMC:

AM = DM (gt).

BM = CM (M là trung điểm của cạnh BC).

\(\widehat{AMB}=\widehat{DMC}\) (Đối đỉnh).

\(\Rightarrow\Delta AMB=\Delta DMC\left(c-g-c\right).\)

b) Xét tam giác ABD và tam giác DCA:

AB = DC \(\left(\Delta AMB=\Delta DMC\right).\)

AD chung.

\(\widehat{BAD}=\widehat{CDA}\) \(\left(\Delta AMB=\Delta DMC\right).\)

\(\Rightarrow\Delta ABD=\Delta DCA\left(c-g-c\right).\)

Xét \(\Delta ABD:AB+BD>AD.\Leftrightarrow AB+BD>2AM.\)

Mà \(BD=AC\) \(\left(\Delta ABD=\Delta DCA\right).\)

\(\Rightarrow AB+AC>2AM.\)