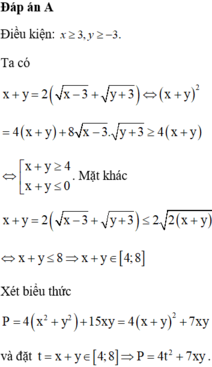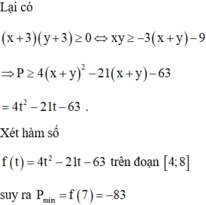Giá trị của x thỏa mãn bất phương trình 2x+6>x+1 là

Những câu hỏi liên quan
Cho bất phương trình 3 - 2x < 15 - 5x và bất phương trình 3 - 2x < 7. Hãy :
a) Giải các bất phương trình đã cho và biểu diễn tập nghiệm của mỗi bất phương trình trên một trục số ( biểu diện hộ luôn đi)
b) Tìm các giá trị nguyên của x thỏa mãn đồng thời cả hai bất phương trình trên ?
Cho hệ phương trình x+my=m+1 mx+y=3m-1 Tìm giá trị của m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x+y
Tìm m để phương trình \(x^2-x+m^2-6=0\) có hai nghiệm \(x_1,x_2\) thỏa mãn \(2018x_1+2019x_2=2020\) Tích các giá trị của m tìm được là
Tập tất cả các giá trị của tham số m để hệ bất phương trình
2
x
-
1
≥
3
x
-
m
≤
0
có nghiệm duy nhất là A.
∅
B. ...
Đọc tiếp
Tập tất cả các giá trị của tham số m để hệ bất phương trình 2 x - 1 ≥ 3 x - m ≤ 0 có nghiệm duy nhất là
A. ∅
B. 2
C. [ 2 ; + ∞ )
D. ( - ∞ ; 2 ]
Ta có 2 x - 1 ≥ 3 x - m ≤ 0 ⇔ x ≥ 2 x ≤ m . Hệ có nghiệm duy nhất khi và chỉ khi m = 2
Đúng 0
Bình luận (0)
Tập hợp các số nguyên x thỏa mãn giá trị tuyệt đối của 2x+3 nhỏ hơn hoặc bằng 5 là ............
Cho hệ phương trình
x+my=m+1
mx+y=3m-1
Tìm giá trị của m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x+y<0
\(\left\{{}\begin{matrix}x+my=m+1\\mx+y=3m-1\end{matrix}\right.\)
Xét \(m=0\) , hệ pt tương đương:
\(\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\Rightarrow x+y=0\left(\text{loại}\right)\)
\(\Rightarrow m\ne0\)
Hệ pt có nghiệm duy nhất khi:
\(\frac{1}{m}\ne m\Leftrightarrow m\ne\pm1\)
Hệ pt tương đương:
\(\left\{{}\begin{matrix}x=m+1-my\\m\left(m+1-my\right)+y=3m-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+1-my\\y\left(m^2-1\right)=\left(m-1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\frac{3m+1}{m+1}\\y=\frac{m-1}{m+1}\end{matrix}\right.\)
\(\Rightarrow x+y=\frac{4m}{m+1}\)
\(x+y< 0\Leftrightarrow\frac{4m}{m+1}< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}4m>0\\m+1>0\end{matrix}\right.\\\left\{{}\begin{matrix}4m< 0\\m+1< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}m>0\\m>-1\end{matrix}\right.\\\left\{{}\begin{matrix}m< 0\\m< -1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m>0\\m< -1\end{matrix}\right.\)
Vậy để hệ phương trình có nghiệm duy nhất \(\left(x;y\right)\) thỏa mãn \(x+y< 0\) thì \(m>0;m< -1;m\ne1\)
Tập tất cả các giá trị của tham số m để bất phương trình m 2 + 3 m x ≤ m 2 nghiệm đúng với mọi x là:
A. (0;1)
B. {0}
C. {0;1}
D. {1}
* Nếu m= 0 thì bất phương trình đã cho trở thành:
0x < 0( luôn đúng với mọi x).
* Nếu m= 1 thì bất phương trình đã cho trở thành:
0x < 1 ( luôn đúng với mọi x)
Tập tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x là {0; 1}
Đúng 0
Bình luận (0)
Cho các số thực x, y thỏa mãn
x
+
y
2
x
-
3
+
y
+
3
. Giá trị nhỏ nhất của biểu thức
P
4
(
x
2
+
y
2
)
+
15
x...
Đọc tiếp
Cho các số thực x, y thỏa mãn x + y = 2 x - 3 + y + 3 . Giá trị nhỏ nhất của biểu thức P = 4 ( x 2 + y 2 ) + 15 x y là:
A. minP = -83
B. minP = -63
C. minP = -80
D. minP = -91
Giả sử phương trình
l
o
g
2
2
x
-
(
m
-
2
)
l
o
g
2
x
+
2
m
0
có hai nghiệm thực phân biệt
x
1
,
x
2
thỏa mãn
x
1...
Đọc tiếp
Giả sử phương trình l o g 2 2 x - ( m - 2 ) l o g 2 x + 2 m = 0 có hai nghiệm thực phân biệt x 1 , x 2 thỏa mãn x 1 + x 2 = 6 . Giá trị của biểu thức x 1 - x 2 là
A.3
B.8
C.2
D.4