Giúp mình làm câu f bài 6 với .

Những câu hỏi liên quan
Hello mng ạ , mng giúp mình kiểm tra mấy bài này làm đúng chưa với ạ và mng giúp luôn mình bài 6 câu 2 ạ
Mình cảm ơn ạ

mình làm những bài bn chưa lm nhé
9B
10A
bài 2
have repainted
bàii 3
ride - walikking
swimming
watch
Đúng 2
Bình luận (1)
2 have repainted
4 have done
8 have stepped
9 have you ever played
7) 1 riding -walking
2 swimming
3 watching
8)
2 my mother doesn't like listening to music
5 doing more exercises makes you healthier
còn lại ok nha
Đúng 1
Bình luận (1)
chịu ???????????????????
Làm giúp mình câu b và câu f với ạ. Mình cần gấp, mình cảm ơn trước
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
Đúng 1
Bình luận (0)
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(=100\cdot\dfrac{\sqrt{3}}{3}\)
\(=\dfrac{100\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=100^2+\left(\dfrac{100\sqrt{3}}{3}\right)^2=\dfrac{40000}{3}\)
hay \(AC=\dfrac{200\sqrt{3}}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giúp mình với câu D, e, f bài 1 với bài 2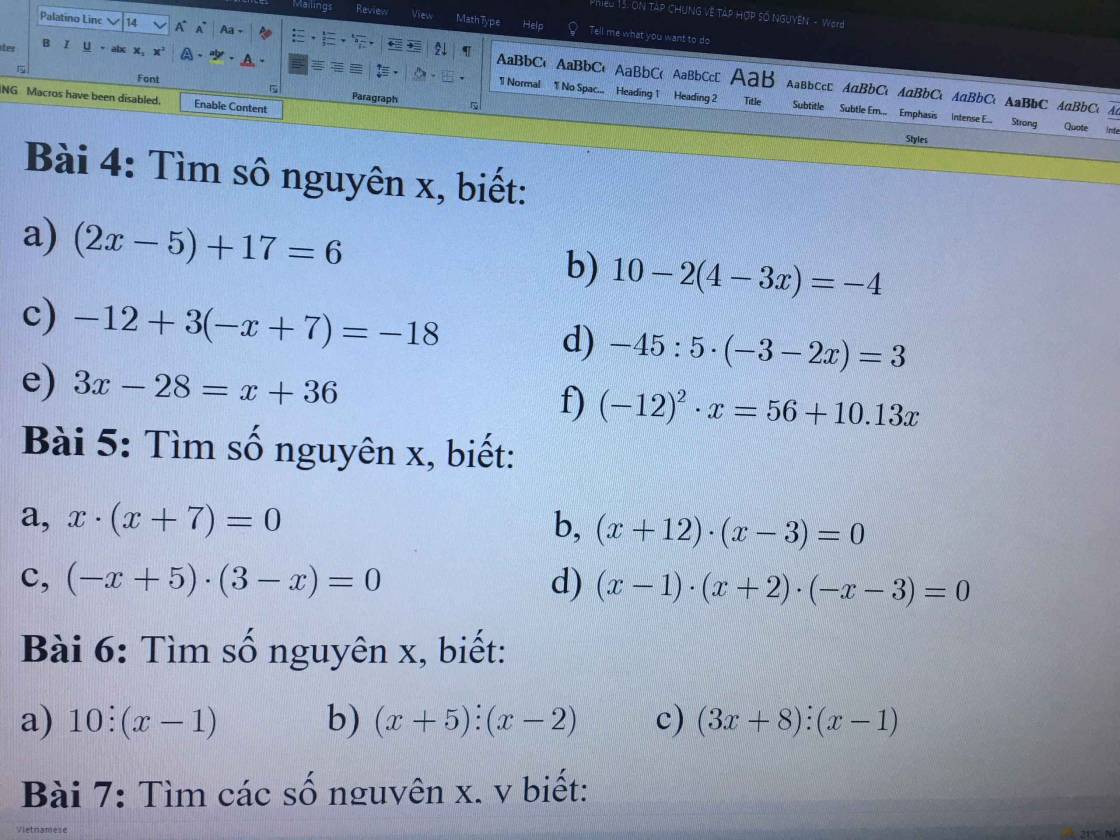
Xem thêm câu trả lời
Dạ mng xem giúp mình mấy bài trắc nghiệm làm đúng chưa với ạ , mng giúp mình luôn câu 5 bài 2 và câu 2 bài 3 ạ
Mình cảm ơn trước ạ


Bài 2
5 C
Bài 3
1 D
6 C
Còn lại ol r nhé
Đúng 2
Bình luận (3)

Làm giúp mình câu c , d , e, f, g ạ .
Thank nha
Đề bài : Viết dứoi dạng bình phưogn tổng hơạc hiệu
c) \(=\left(5a-\dfrac{1}{3}\right)^2\)
d) \(=\left(y-\dfrac{1}{3}\right)^2\)
e) \(=\left(2x-y+1\right)^2\)
f) \(=\left(2x-4y\right)^2+2\left(2x-4y\right)+1=\left(2x-4y+1\right)^2\)
g) \(=\left(2xy^2-3\right)^2\)
Đúng 1
Bình luận (0)
\(c,=\left(5a-\dfrac{1}{3}\right)^2\\ d,=\left(y^4-\dfrac{1}{3}\right)^2\\ e,=\left(2x-y+1\right)^2\\ f,=\left(2x-4y\right)^2+4\left(x-2y\right)+1=\left(2x-4y+1\right)\\ g,=\left(2xy^2-3\right)^2\)
Đúng 2
Bình luận (1)
mn làm giúp mình bài đó với làm câu a,b 
a) Do \(\dfrac{R1}{R2}=\dfrac{R3}{R4}\) nên mạch là mạch cầu cân bằng.
=> Cường độ dòng điện qua ampe kế là \(IA=0\left(A\right)\)
b) Gọi cường độ dòng điện qua các điện trở R1,R2,R3,R4 lần lượt là \(I1,I2,I3,I4\) , cường độ dòng điện qua ampe kế là \(IA'\)
Do dòng điện qua ampe kế có chiều từ M->N và có cường độ 0,2 A nên ta có:
\(I1-I3=IA'=0,2\left(A\right)\) (1)
Điện trở tương đương của mạch là:
\(Rtđ=\dfrac{R1.R2}{R1+R2}+\dfrac{R3.R4}{R3+R4}=\dfrac{10.15}{10+15}+\dfrac{12R4}{12+R4}=6+\dfrac{12R4}{12+R4}=\dfrac{72+18R4}{12+R4}\)
=> Cường độ dòng điện mạch chính là:
\(I=\dfrac{U}{Rtđ}=\dfrac{12\left(12+R4\right)}{72+18R4}=\dfrac{24+2R4}{12+3R4}\)
Cường độ dòng điện chạy qua R1 là:
\(I1=\dfrac{R2}{R1+R2}.I=\dfrac{2}{5}I\)
=>\(I3=\dfrac{R4}{R4+R3}.I=\dfrac{R4}{R4+12}I\)
=>\(IA'=\left(\dfrac{2}{5}-\dfrac{R4}{12+R4}\right)I\)
Sau đó bạn chỉ cần thay vào là tính đc nhé![]()
Đúng 0
Bình luận (0)
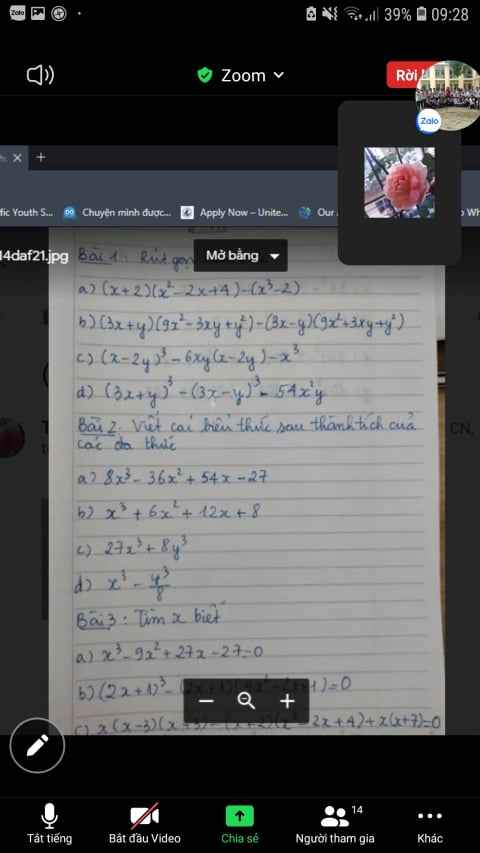
làm giúp mình bài 2 với câu d bài 1 vs ạ
Bài 2:
a: \(8x^3-36x^2+54x-27=\left(2x-3\right)^3\)
b: \(x^3+6x^2+12x+8=\left(x+2\right)^3\)
c: \(27x^3+8y^3=\left(3x+2y\right)\left(9x^2-6xy+4y^2\right)\)
d: \(x^3-\dfrac{y^3}{8}=\left(x-\dfrac{1}{2}y\right)\left(x^2+\dfrac{1}{2}xy+\dfrac{1}{4}y^2\right)\)
Đúng 2
Bình luận (0)
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
Đọc tiếp
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 4
Bình luận (0)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Đúng 1
Bình luận (0)
giúp mình câu ioe phần nghe (làm bài thi 4) vòng 14 lớp 6 với
does she brush shoes ********* ? ( 9 kí tự )
điền vào các chữ r-e-g-u-l-a-r-l-y
100% đúng
Đúng 4
Bình luận (0)
Xem thêm câu trả lời
Làm giúp mình 5 câu cuối bài 1 và bài 2 với ạ

6) \(\dfrac{8^6}{256}=\dfrac{\left(2^3\right)^6}{2^8}=\dfrac{2^{18}}{2^8}=2^{10}=1024\)
7) \(\left(\dfrac{1}{2}\right)^{15}.\left(\dfrac{1}{4}\right)^{20}=\left(\dfrac{1}{2}\right)^{15}.\left[\left(\dfrac{1}{2}\right)^2\right]^{20}=\left(\dfrac{1}{2}\right)^{15}.\left(\dfrac{1}{2}\right)^{40}=\left(\dfrac{1}{2}\right)^{55}=\dfrac{1}{2^{55}}\)
8) \(\left(\dfrac{1}{9}\right)^{25}\div\left(\dfrac{1}{3}\right)^{30}=\left(\dfrac{1}{3}\right)^{50}\div\left(\dfrac{1}{3}\right)^{30}=\left(\dfrac{1}{3}\right)^{20}=\dfrac{1}{3^{20}}\)
9)\(\left(\dfrac{1}{16}\right)^3\div\left(\dfrac{1}{8}\right)^2=\left(\dfrac{1}{2}\right)^{12}\div\left(\dfrac{1}{2}\right)^6=\left(\dfrac{1}{2}\right)^6=\dfrac{1}{64}\)
10) \(\dfrac{27^2.8^5}{6^2.32^3}=\dfrac{3^6.2^{15}}{3^2.2^2.2^{15}}=\dfrac{3^4}{2^2}=\dfrac{81}{4}\)
Đúng 0
Bình luận (0)































